chứng tỏ:
câu1
6100-1 chia hết cho 5
câu2
2120-1110 chia hết cho 2 và 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
25 tháng 10 2021
a, 6100 - 1 = (6 . 6 . 6 ..... 6) - 1 = [(...6) . (...6) . (...6) ..... (...6)] - 1 = (...6) - 1 = ...5 \(⋮\) 5
LM
25 tháng 10 2021
b, 2120 - 1110 = (21 . 21 . 21 . 21 . 21..... 21) - (11 . 11 . 11 . 11 ..... 11) = [(...1) . (...1) . (...1) . (...1).....(...1)] - [(...1) . (...1) . (...1) . (...1).....(...1)] = (...1) - (...1) = ....0 \(⋮\) 2; \(⋮\) 5
NT
2
21 tháng 2 2021
Ta có: \(A=2+2^2+2^3+...+2^{120}\)
\(=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{118}+2^{119}+2^{120}\right)\)
\(=14+2^3\cdot14+...+2^{117}\cdot14\)
\(=14\cdot\left(1+2^3+...+2^{117}\right)⋮7\)
Ta có: \(A=2+2^2+2^3+...+2^{120}\)
\(=\left(2+2^2+2^3+2^4+2^5\right)+\left(2^6+2^7+2^8+2^9+2^{10}\right)+...+\left(2^{116}+2^{117}+2^{118}+2^{119}+2^{120}\right)\)
\(=62+2^5\cdot62+...+2^{115}\cdot62\)
\(=62\cdot\left(1+2^5+...+2^{115}\right)⋮31\)
Ta có: \(A=2+2^2+2^3+...+2^{120}\)
\(=\left(2+2^2+2^3+2^4+2^5+2^6\right)+\left(2^7+2^8+2^9+2^{10}+2^{11}+2^{12}\right)+...+\left(2^{115}+2^{116}+2^{117}+2^{118}+2^{119}+2^{120}\right)\)
\(=126+126\cdot2^6+...+126\cdot2^{114}\)
\(=126\cdot\left(1+2^6+...+2^{114}\right)⋮21\)
HV
0
19 tháng 12 2021
\(1,8^8+2^{20}=2^{24}+2^{20}=2^{20}\left(2^4+1\right)=2^{20}\cdot17⋮17\)
\(2,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{119}+2^{120}\right)\\ A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{119}\left(1+2\right)\\ A=3\left(2+2^3+...+2^{119}\right)⋮3\)
\(A=\left(2+2^2+2^3\right)+...+\left(2^{118}+2^{119}+2^{120}\right)\\ A=2\left(1+2+2^2\right)+...+2^{118}\left(1+2+2^2\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{118}\right)=7\left(2+...+2^{118}\right)⋮7\\ A=\left(2+2^2+2^3+2^4\right)+...+\left(2^{117}+2^{118}+2^{119}+2^{120}\right)\\ A=2\left(1+2+2^2+2^3\right)+...+2^{117}\left(1+2+2^2+2^3\right)\\ A=\left(1+2+2^2+2^3\right)\left(2+...+2^{117}\right)=15\left(2+...+2^{117}\right)⋮15\)
CM
26 tháng 5 2017
Ta có; 1110 = (10+1)10 ( khai triển nhị thức Niu- tơn )
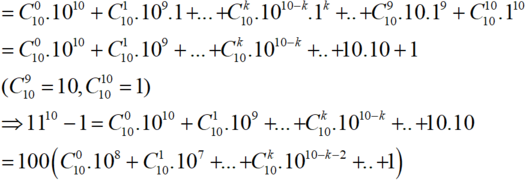
Do đó 1110 -1 chia hết cho 100
VH
2
5 tháng 11 2021
\(A=\left(2+2^2+2^3\right)+...+\left(2^{118}+2^{119}+2^{120}\right)\\ A=2\left(1+2^2+2^3\right)+...+2^{118}\left(1+2^2+2^3\right)\\ A=\left(1+2^2+2^3\right)\left(2+...+2^{118}\right)\\ A=7\left(2+...+2^{118}\right)⋮7\)
5 tháng 11 2021
\(A=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{118}\left(1+2+2^2\right)\)
\(=2.7+2^4.7+...+2^{118}.7=7\left(2+2^4+...+2^{118}\right)⋮7\)
NB
0
câu 1:
Vì tận cùng chúng là chữ số 5 =>nó chia hết cho5.
câu 2
Vi tận cùng bằng 0=>nó chia hết cho 2;5.