Làm giúp mình câu a,b với ạ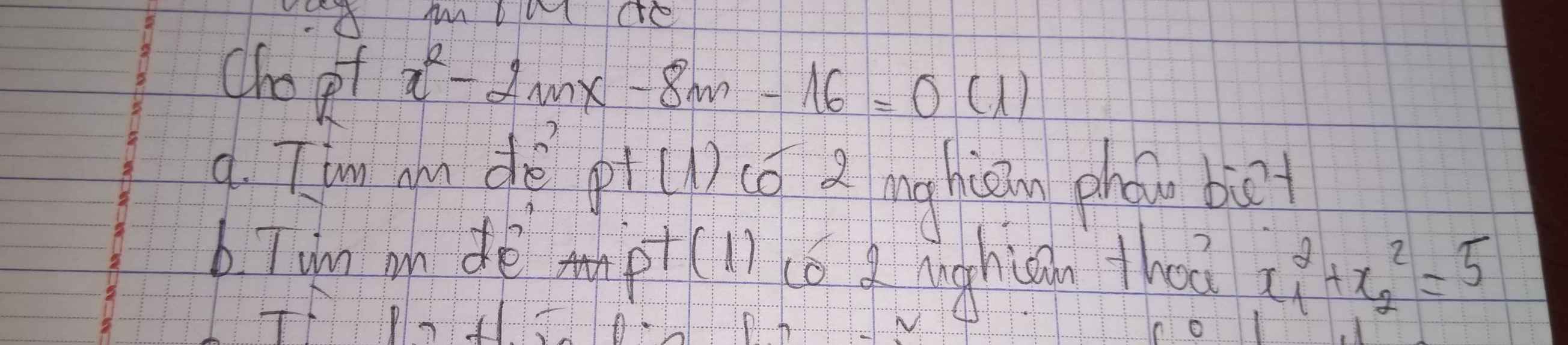
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)

b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm

b: ΔOAH cân tại O(Do A,H cùng nằm trên (O))
mà OD là đường cao
nên OD là phân giác của góc AOH
Xét ΔOAD và ΔOHD có
OA=OH
góc AOD=góc HOD
OD chung
Do đó: ΔOAD=ΔOHD
=>góc OHD=góc OAD=90 độ
=>DH vuông góc OH



\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$





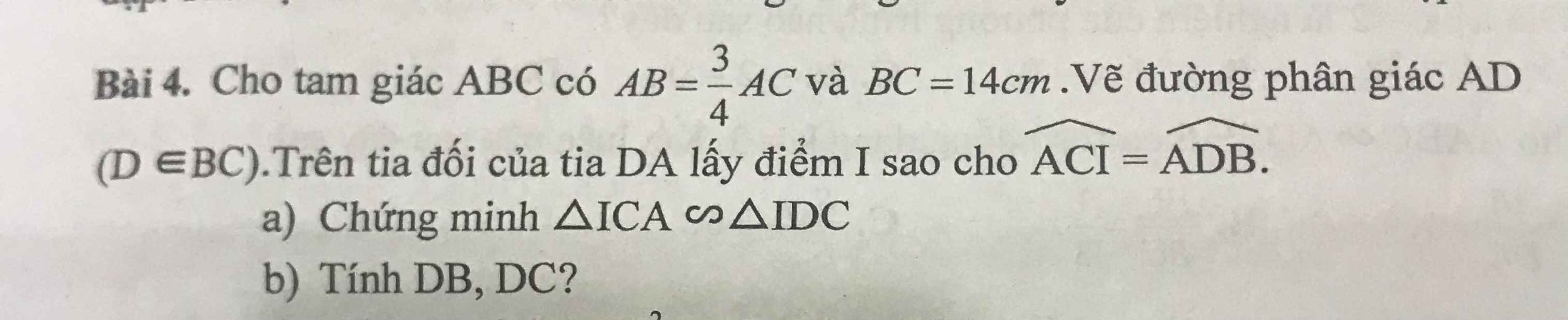





a/ Pt có 2 nghiệm phân biệt
\(\to\Delta'=(-m)^2-1.(-8m-16)=m^2+8m+16=(m+4)^2>0\\\to m+4>0\quad or\quad m+4<0\\\to m>-4\quad or\quad m<-4\)
b/ Theo Vi-ét:
\(\begin{cases}x_1+x_2=2m\\x_1x_2=-8m-16\end{cases}\)
\(x_1^2+x_2^2=5\\\leftrightarrow x_1^2+2x_1x_2+x_2^2-2x_1x_2=5\\\leftrightarrow (x_1+x_2)^2-2x_1x_2=5\\\leftrightarrow (2m)^2-2.(-8m-16)=5\\\leftrightarrow 4m^2+16m+32=5\\\leftrightarrow 4(m^2+4m+8)=5\\\leftrightarrow 4(m+2)^2+16=5\\\leftrightarrow 4(m+2)^2+11=0(\text{vô lý})\\\to m\in\varnothing\)
Vậy không có giá trị m thỏa mãn