Tìm Giá trị lớn nhất A =(4x^2+8x+18)/(x^2+2x+3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: \(-x^2+2x-2=-\left(x-1\right)^2-1\le-1\forall x\)
\(\Leftrightarrow V\ge-1\forall x\)
Dấu '=' xảy ra khi x=1

Bài 1:
a: \(A=x^2+2x+4\)
\(=x^2+2x+1+3\)
\(=\left(x+1\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x+1=0
=>x=-1
Vậy: \(A_{min}=3\) khi x=-1
b: \(B=x^2-20x+101\)
\(=x^2-20x+100+1\)
\(=\left(x-10\right)^2+1>=1\forall x\)
Dấu '=' xảy ra khi x-10=0
=>x=10
Vậy: \(B_{min}=1\) khi x=10
c: \(C=x^2-2x+y^2+4y+8\)
\(=x^2-2x+1+y^2+4y+4+3\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x-1=0 và y+2=0
=>x=1 và y=-2
Vậy: \(C_{min}=3\) khi (x,y)=(1;-2)
Bài 2:
a: \(A=5-8x-x^2\)
\(=-\left(x^2+8x\right)+5\)
\(=-\left(x^2+8x+16-16\right)+5\)
\(=-\left(x+4\right)^2+16+5=-\left(x+4\right)^2+21< =21\forall x\)
Dấu '=' xảy ra khi x+4=0
=>x=-4
b: \(B=x-x^2\)
\(=-\left(x^2-x\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
c: \(C=4x-x^2+3\)
\(=-x^2+4x-4+7\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7< =7\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
d: \(D=-x^2+6x-11\)
\(=-\left(x^2-6x+11\right)\)
\(=-\left(x^2-6x+9+2\right)\)
\(=-\left(x-3\right)^2-2< =-2\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3

a: \(-2x^2-8x+1\)
\(=-2x^2-8x-8+9\)
\(=-2\left(x^2+4x+4\right)+9\)
\(=-2\left(x+2\right)^2+9< =9\forall x\)
Dấu '=' xảy ra khi x+2=0
=>x=-2
b: \(-5x^2-y^2-4xy+4x+3\)
\(=\left(-4x^2-4xy-y^2\right)+\left(-x^2+4x-4\right)+7\)
\(=-\left(2x+y\right)^2-\left(x-2\right)^2+7< =7\forall x,y\)
Dấu '=' xảy ra khi 2x+y=0 và x-2=0
=>x=2 và y=-2x=-4

A = x2 + 4x + 7
= ( x2 + 4x + 4 ) + 3
= ( x + 2 )2 + 3
( x + 2 )2 ≥ 0 ∀ x => ( x + 2 )2 + 3 ≥ 3
Đẳng thức xảy ra <=> x + 2 = 0 => x = -2
=> MinA = 3 <=> x = -2
B = 2x2 - 6x
= 2( x2 - 3x + 9/4 ) - 9/2
= 2( x - 3/2 )2 - 9/2
2( x - 3/2 )2 ≥ 0 ∀ x => 2( x - 3/2 )2 -9/2 ≥ -9/2
Đẳng thức xảy ra <=> x - 3/2 = 0 => x = 3/2
=> MinB = -9/2 <=> x = 3/2
C = -2x2 + 8x - 15
= -2( x2 - 4x + 4 ) - 7
= -2( x - 2 )2 - 7
-2( x - 2 )2 ≤ 0 ∀ x => -2( x - 2 )2 - 7 ≤ -7
Đẳng thức xảy ra <=> x - 2 = 0 => x = 2
=> MaxC = -7 <=> x = 2


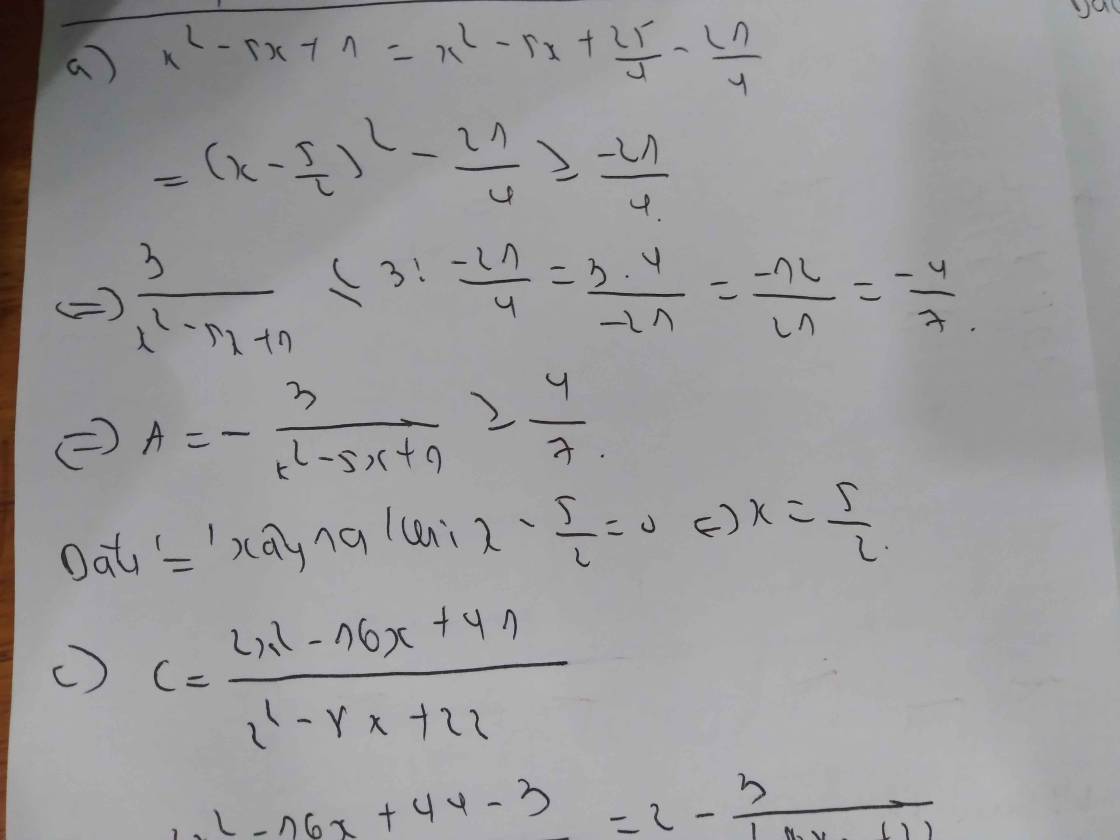
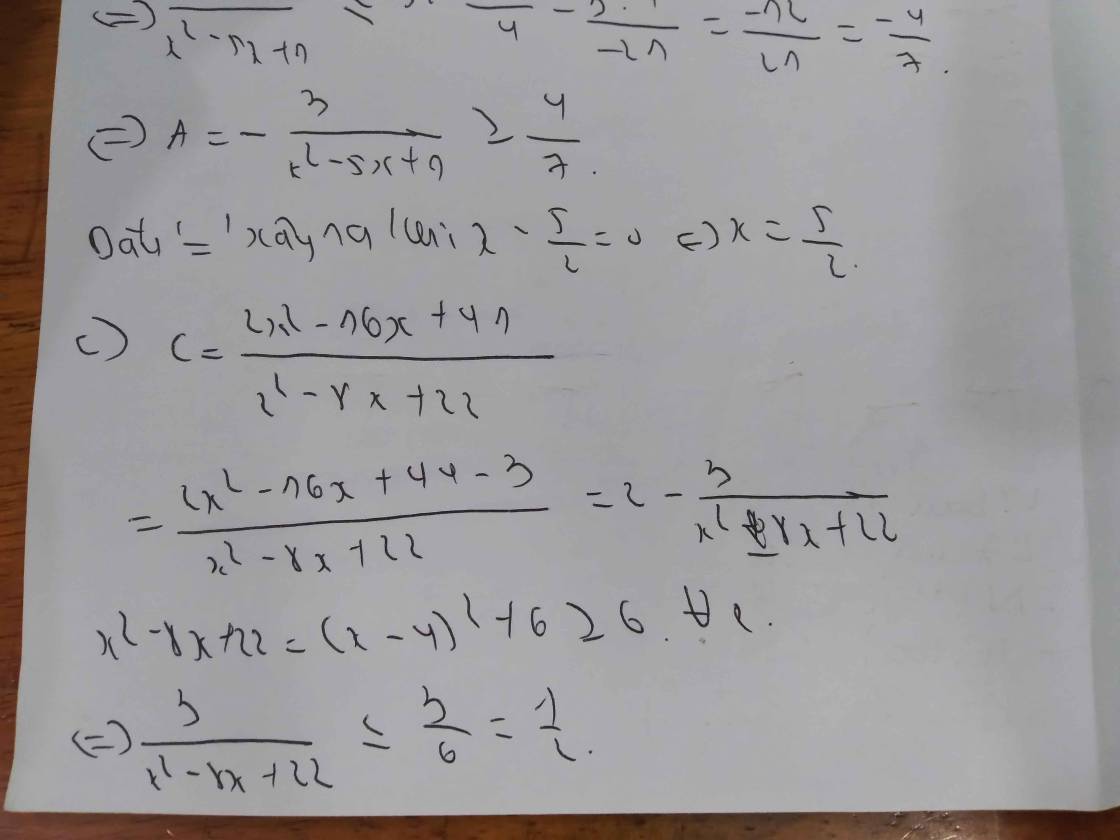
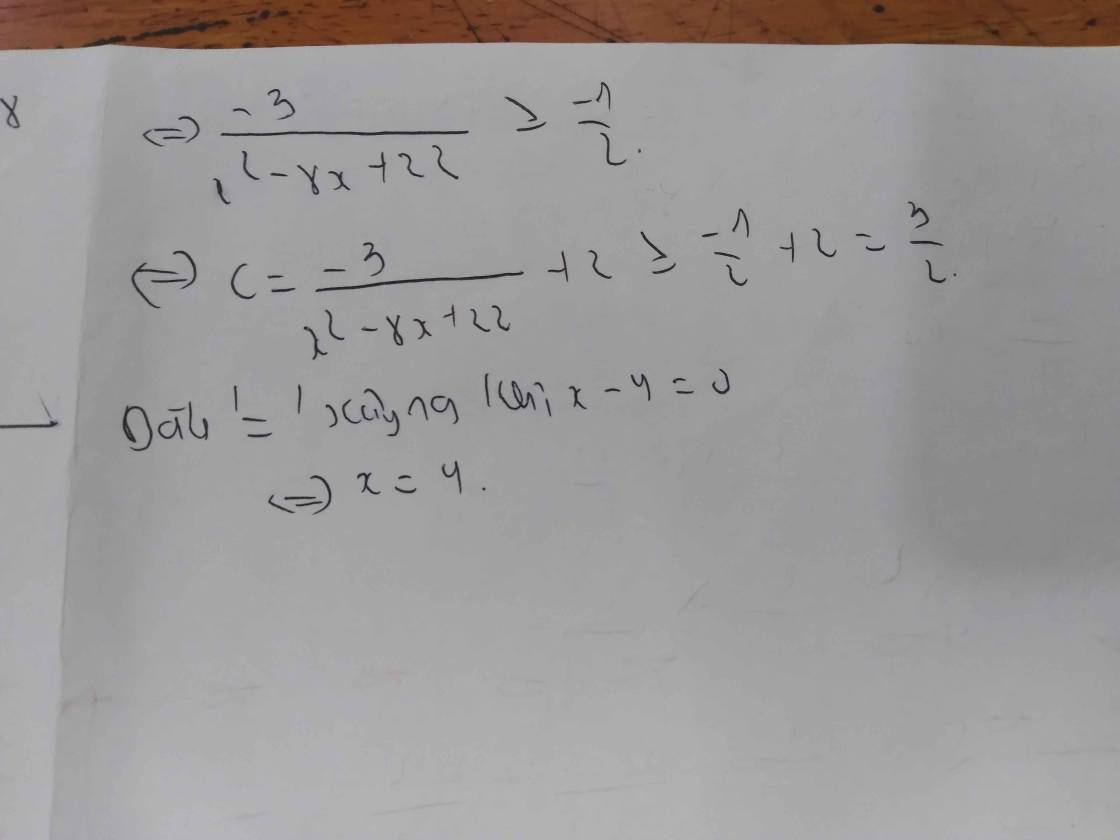
\(A=\dfrac{4\left(x^2+2x+3-3\right)+18}{x^2+2x+3}=\dfrac{4\left(x^2+2x+3\right)+6}{x^2+2x+3}=4+\dfrac{6}{\left(x+1\right)^2+2}\)
Ta có \(\left(x+1\right)^2+2\ge2\Rightarrow\dfrac{6}{\left(x+1\right)^2+2}\le3\Leftrightarrow4+\dfrac{6}{\left(x+1\right)^2+2}\le7\)
Dấu ''='' xảy ra khi x = -1
=\(\dfrac{18}{7}\)