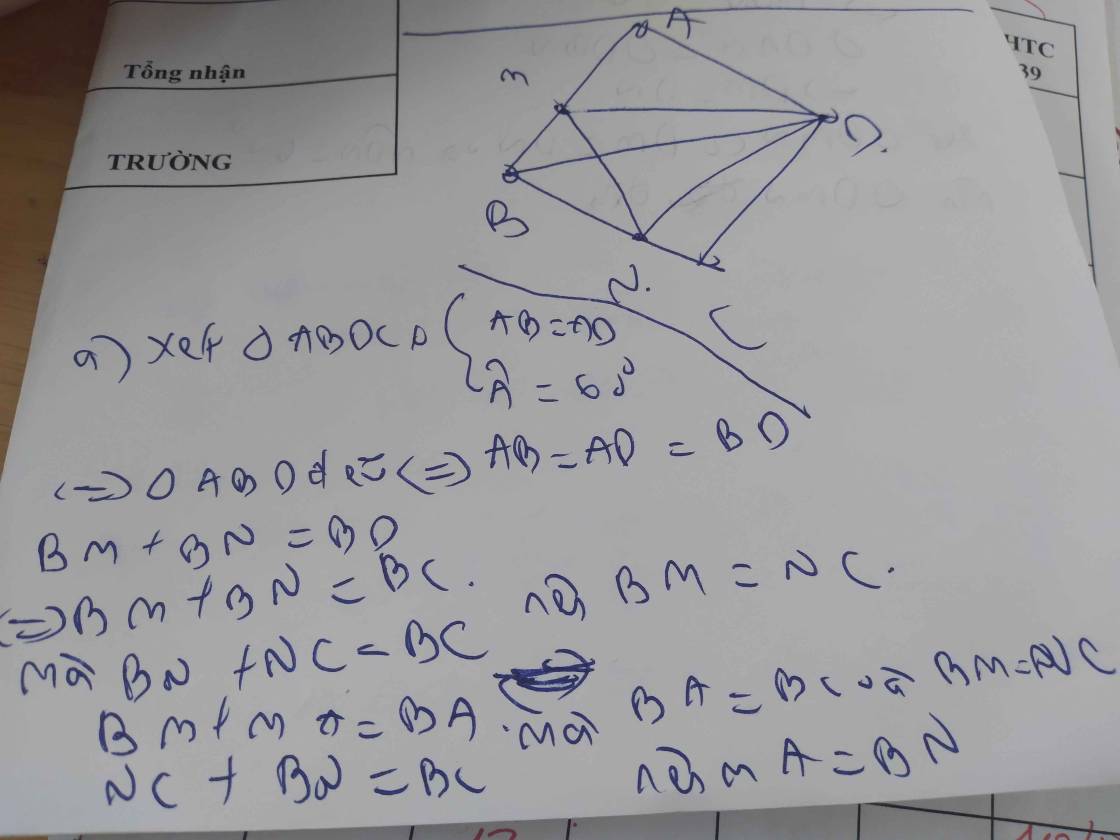
Cho hình thoi ABCD có góc A = 60o Đường thằng d cắt 2 cạnh AB, BC lần lượt tại M,N sao cho MB + NB = CD. Chứng minh rằng tam giác DMN đều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 1 2019
Ta có : MB+NB=AB=MB+AM
Suy ra : NB=AM
Tương tự : BM=NC
Ta có: \(\widehat{A}=60o\)
Suy ra: \(\widehat{D}=180o-\widehat{A}=120o\)
Dễ thấy, tam giác BMD=tam giác CND (c.g.c)
\(=>\left\{{}\begin{matrix}MD=ND\left(1\right)\\\widehat{BDM}=\widehat{CDN}\end{matrix}\right.\)
Ta có: \(\widehat{BDN}+\widehat{CDN}=60o=>\widehat{BDN}+\widehat{BDM}=60o\)
Hay \(\widehat{MDN}=60o\left(2\right)\)
Từ (1) và (2) => Tam giác MDN là tam giác đều
Chứ o ở sau các số là độ nha bn, mk ko bik cách gõ nên gõ tạm chữ o.
Chúc bn học tốt!
CM
23 tháng 4 2019
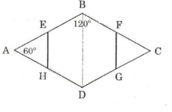
+ ABCD là hình thoi
⇒ AD // BC
+ ABCD là hình thoi ⇒ AB = BC = CD = DA
Mà E, F, G, H là trung điểm của 4 đoạn thẳng trên
⇒ AE = EB = BF = FC = CG = GD = DH = HA.
ΔAEH có góc A = 60º và AE = AH nên là tam giác đều
+ Lại có ΔAEH đều
⇒ EH = AH = AE.
Chứng minh tương tự : FG = FC = CG
⇒ EB = BF = FG = GD = DH = HE.
Vậy EBFGDH có tất cả các góc bằng nhau và tất cả các cạnh bằng nhau nên là lục giác đều.
HM
1
27 tháng 11 2021
\(\left\{{}\begin{matrix}MB+NB=AB\\MB+AM=AB\end{matrix}\right.\Rightarrow NB=AM\\ ABCD\text{ là hthoi }\Rightarrow AB=AD\\ \text{Mà }\widehat{A}=60^0\\ \Rightarrow\Delta ABD\text{ đều}\\ \Rightarrow AB=AD=BD\\ ABCD\text{ là hthoi}\\ \Rightarrow AD\text{//}BC\Rightarrow\widehat{ABC}=120^0\\ \text{Mà }BD\text{ là p/g }\widehat{ABC}\\ \Rightarrow\widehat{DBN}=\dfrac{1}{2}\widehat{ABC}=60^0\\ \left\{{}\begin{matrix}NB=AM\\\widehat{DBN}=\widehat{A}=60^0\\AD=BD\end{matrix}\right.\Rightarrow\Delta DAM=\Delta DBN\left(c.g.c\right)\\ \Rightarrow DM=DN;\widehat{ADM}=\widehat{BDN}\left(1\right)\\ \Rightarrow\Delta DMN\text{ cân tại }D\\ \left(1\right)\Rightarrow\widehat{ADM}+\widehat{MDB}=\widehat{BDN}+\widehat{MDB}\\ \Rightarrow\widehat{MDN}=\widehat{ADB}=60^0\left(\Delta ABD\text{ đều}\right)\\ \Rightarrow\Delta DMN\text{ đều}\)
CM
22 tháng 12 2019
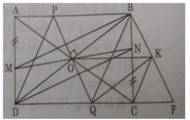
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.
