cho (P ): y= x^2 và (d) : y=4x-3
a/ Vẽ đồ thị (P)
b/ Xác định tọa độ các giao điểm của (P) và (d) bằng phép tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-3=-3x+2\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

Từ Phương trình hoành độ giao điểm sẽ tìm được tọa độ của A ( x1,y1) và B (x2 , y2)
Bạn Vẽ hình . Gọi M là hình chiếu của A trên Ox , N là Hình chiếu của B trên Ox . tiếp theo bạn tính lần lượt các diện tích sau.:
1. S tam giác AMO vuông tại M
2. S tam giác BNO vuông tại N
3. S Hình Thang AMNB .
=> S tam giác AOB = S Hình thang AMNB - ( S tam giác AMO + S tam giác BNO)

b: Toạ độ giao điểm của (d) và (d1) là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x+5=-\dfrac{3}{2}x+1\\y=\dfrac{1}{2}x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-4\\y=\dfrac{1}{2}x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=\dfrac{1}{2}\cdot\left(-2\right)+5=5-1=4\end{matrix}\right.\)

a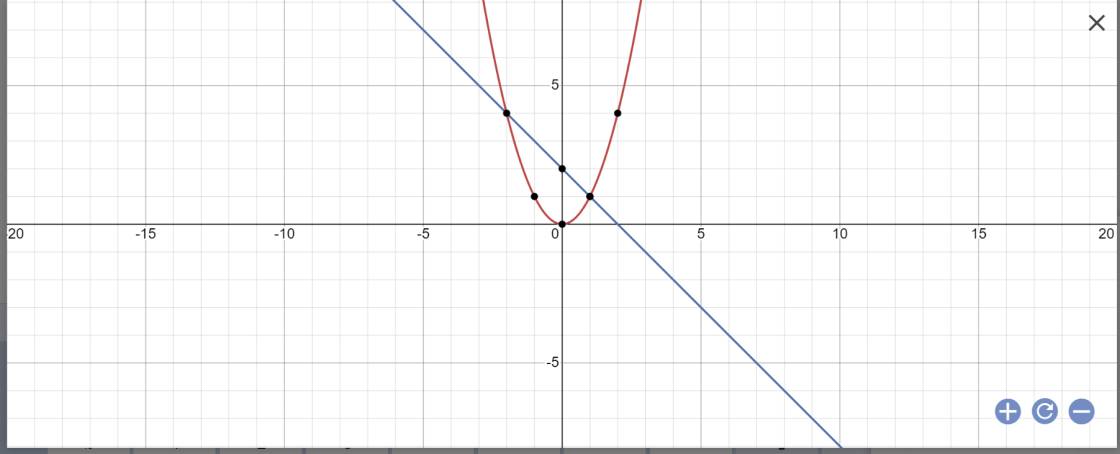
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

b: Tọa độ giao điểm của (d) và (d1) là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x+5=\dfrac{-3}{2}x+1\\y=\dfrac{1}{2}x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-4\\y=\dfrac{1}{2}x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1+5=4\end{matrix}\right.\)
a)
Đồ thị:
b) Phương trình hoành độ giao điểm của (P) và (d):
\(x^2=4x-3\)
\(\Leftrightarrow x^2-4x+3=0\)
Ta có: \(a+b+c=1+\left(-4\right)+3=0\)
\(\Rightarrow x_1=1;x_2=3\)
Với \(x_1=1\Rightarrow y_1=1\Rightarrow M\left(1;1\right)\)
Với \(x_2=3\Rightarrow y_2=9\Rightarrow N\left(3;9\right)\)
Vậy tọa độ giao điểm của (P) và (d) là: M(1; 1) và N(3; 9)