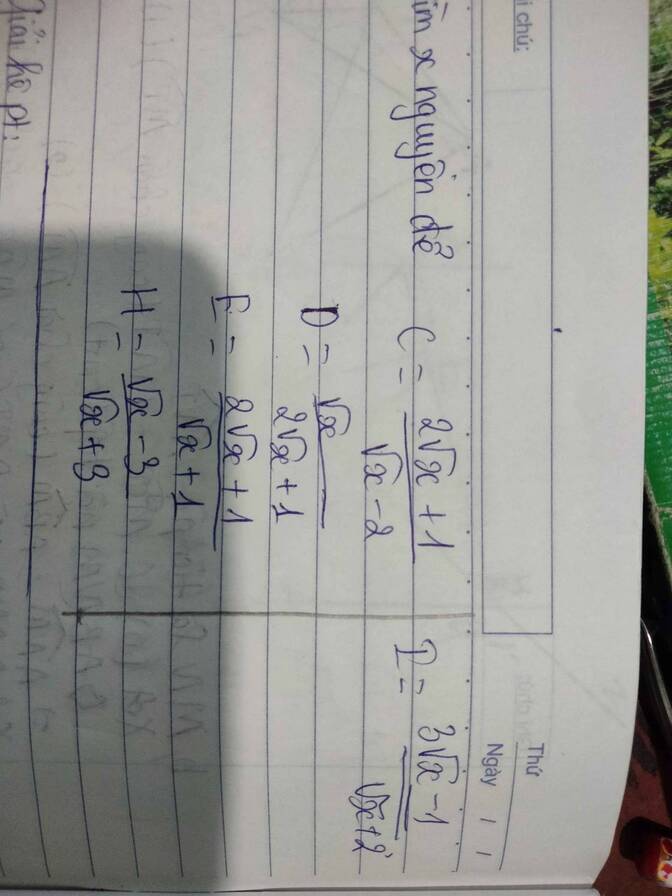Tìm x để bt nguyê
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2018
\(A=\frac{x-3}{x+1}\)
a,
\(A=\frac{x-3}{x+1}=\frac{1}{5}\)
\(\Leftrightarrow\left(x-3\right)\cdot5=1\cdot\left(x+1\right)\)
\(\Leftrightarrow5x-15=x+1\)
\(\Leftrightarrow5x-x=1+15\)
\(\Leftrightarrow4x=16\)
\(\Leftrightarrow x=4\)
vậy A = 1/5 khi x = 4
\(b,A=\frac{x-3}{x+1}\inℤ\Leftrightarrow x-3⋮x+1\)
\(\Rightarrow x+1-4⋮x+1\)
\(x+1⋮x+1\)
\(\Rightarrow4⋮x+1\)
\(\Rightarrow x+1\inƯ\left(4\right)=\left\{-1;1;-2;2;-4;4\right\}\)
\(\Rightarrow x\in\left\{-2;0;-3;1;-5;3\right\}\)
vậy A nguyên khi x = -2; 0; -3; 1; -5; 3
\(c,A=\frac{x-3}{x+1}=\frac{x+1-4}{x+1}=1-\frac{4}{x+1}\)
để A đạt GTLN thì \(\frac{4}{x+1}\) nhỏ nhất
=> x + 1 lớn nhất
=> A không có GTLN
NH
1
8 tháng 5 2016
-4 chia hết cho 2x-1, có:2x-1 là U(-4)=-4;-1;1;4
2x-1=-4, có x không thuộc Z
2x-1=-1, có x=0
2x-1=1, có x=1
2x-1=4, có x không thuộc Z
Vậy x=0;1
HP
18 tháng 12 2021
a, ĐK: \(x\ge0,x\ne1\)
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(=\dfrac{x+1+2\sqrt{x}+x+1-2\sqrt{x}-3\sqrt{x}-1}{x-1}\)
\(=\dfrac{2x-3\sqrt{x}+1}{x-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
16 tháng 3 2020
\(3x+\frac{1}{7}=x+\frac{2}{4}\)
\(3x-x=\frac{1}{2}-\frac{1}{7}\)
\(2x=\frac{5}{14}\)
\(x=\frac{5}{14}:2\)
\(x=\frac{5}{28}\)
KD
0
DD
Đoàn Đức Hà
Giáo viên
29 tháng 11 2021
Điều kiện xác định của \(P\)là:
\(\hept{\begin{cases}x^2+2x+1\ne0\\x^2-1\ne0\\x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\pm1\\x\ne0\end{cases}}\)
\(P=\left(\frac{2+x}{x^2+2x+1}-\frac{x-2}{x^2-1}\right).\frac{1-x^2}{x}\)
\(=\left[\frac{\left(x+2\right)\left(x-1\right)}{\left(x+1\right)^2\left(x-1\right)}-\frac{\left(x-2\right)\left(x+1\right)}{\left(x+1\right)^2\left(x-1\right)}\right].\frac{1-x^2}{x}\)
\(=\frac{2x}{\left(x+1\right)^2\left(x-1\right)}.\frac{1-x^2}{x}=\frac{-2}{x+1}\)
Để \(P\)nguyên mà \(x\)nguyên suy ra \(x+1\inƯ\left(2\right)=\left\{-2,-1,1,2\right\}\Leftrightarrow x\in\left\{-3,-2,0,1\right\}\)
Đối chiếu điều kiện ta được \(x\in\left\{-3,-2\right\}\)thỏa mãn.
B
0
DL
1
13 tháng 7 2017
5/x = 1/8 - y/4 = 1-2y/8 <=> x = 5*8/1-2y
ta thấy 1-2y là số lẻ nên UCLN(8; 1-2y)=1 do đó x/8=5/1-2y
x,y nguyên khi 1-2y phải là ước của 5
* 1-2y = -1 => y =1 => x = -40
* 1-2y = 1 => y = 0 => x= 40
*1-2y = -5 => y = 3 => x = -8
* 1-2y = 5 => y = -2 => x= 8
vậy có 4 cặp x,y nguyên ( -40,1) (40,0) (-8,-5) (8,5)
nhớ mk nhá