giả sử x1;x2 là hai nghiệm của phương trình bậc hai: x2 - 3\(\sqrt{2}\)x - \(\sqrt{2}\)=0
tính giá trị biểu thức \(A=\frac{2}{3\sqrt{2}x_1+x_2^2-3\sqrt{2}}+\frac{3\sqrt{2}.x_2+x_1^2-3\sqrt{2}}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DK
1
20 tháng 1 2021
nhiệm là cái gì? Đề ko rõ nữa vì M = (1 - x2)x1 + (1 - x1)x2 chả có gì để cm cả :v
CM
24 tháng 12 2017
Giả sử x 1 , x 2 la hai nghiệm của phương trình x 2 + px + q = 0
Theo hệ thức Vi-ét ta có: x 1 + x 2 = - p/1 = - p; x 1 x 2 = q/1 = q
Phương trình có hai nghiệm là x 1 + x 2 và x 1 x 2 tức là phương trình có hai nghiệm là –p và q.
Hai số -p và q là nghiệm của phương trình.
(x + p)(x - q) = 0 ⇔ x 2 - qx + px - pq = 0 ⇔ x 2 + (p - q)x - pq = 0
Phương trình cần tìm: x 2 + (p - q)x - pq = 0
CM
25 tháng 12 2017
Chọn đáp án C
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Đặt ẩn phụ để giải phương trình: log 2 x = t . Tìm điều kiện để phương trình có nghiệm.
+) Dựa vào dữ kiện x 1 + x 2 = 6 tìm m. Từ đó tính x 1 - x 2 .
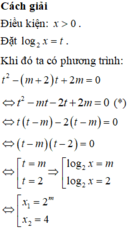
Phương trình đã cho có hai nghiệm phân biệt: x 1 , x 2 ⇔ phương trình (*) có hai nghiệm phân biệt ⇔ m ≠ 2 .
CM
25 tháng 3 2018
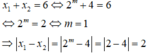
Giả sử x 1 , x 2 là hai nghiệm của phương trình bậc hai a x 2 + bx + c = 0 có ∆’ = 0
Do đó, phương trình có nghiệm kép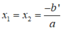 
Chọn B
CM
21 tháng 10 2019
Phương trình 2 x 2 - 4 m x - 1 = 0 có ∆ ' = 4 m 2 + 2 > 0 nên phương trình có hai nghiệm phân biệt x 1 , x 2 với S = x 1 + x 2 = 2 m , P = x 1 x 2 = - 1 2
Ta có: T 2 = x 1 - x 2 2 = S 2 - 4 P = 4 m 2 + 2 ≥ 2 ⇒ T ≥ 2
Dấu bằng xảy ra khi m = 0.
Vậy m i n T = 2
Đáp án cần chọn là: B
x1;x2 là nghiệm của pt
=> \(x^2_1-3\sqrt{2}x_1-\sqrt{2}=0\Rightarrow x^2_1=3\sqrt{2}x_1+\sqrt{2}\)
\(x^2_2-3\sqrt{2}x_2-\sqrt{2}=0\Rightarrow x^2_2=3\sqrt{2}x_2+\sqrt{2}\)
=> \(A=\frac{2}{3\sqrt{2}x_1+3\sqrt{2}x_2+\sqrt{2}-3\sqrt{2}}+\frac{3\sqrt{2}x_2+3\sqrt{2}x_1+\sqrt{2}-3\sqrt{2}}{2}\)
\(A=\frac{2}{3\sqrt{2}\left(x_1+x_2\right)-2\sqrt{2}}+\frac{3\sqrt{2}\left(x_2+x_1\right)-2\sqrt{2}}{2}\)
Theo VI ét => \(x_1+x_2=3\sqrt{2}\). Thay vào A
=> quy đồng.....