Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
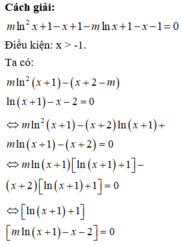
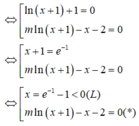

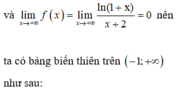


a)\(\Delta'=\left[\frac{-2.\left(m-1\right)}{2}\right]^2-m^2=m^2-2m+1-m^2=-2m+1\)
b)Để PT có hai nghiệm phân biệt thì \(\Delta'=-2m+1>0\Rightarrow m<\frac{1}{2}\)
Để PT có nghiệm kép thì: \(\Delta'=-2m+1=0\Rightarrow m=\frac{1}{2}\)
Để PT vô nghiệm thì: \(\Delta'=-2m+1<0\Rightarrow m>\frac{1}{2}\)

Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
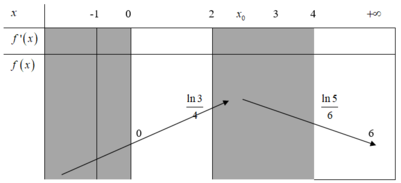
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .

Bài 1:
\(\Delta=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
=>-4m>-13
hay m<13/4
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=6\\2x_1-5x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x_2=14\\x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2\\x_1=1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-1\)
nên m-1=2
hay m=3
Bài 2:
\(\Delta=\left(2m-4\right)^2-4\cdot\left(-2m+1\right)\)
\(=4m^2-16m+16+8m-4\)
\(=4m^2-8m+12\)
\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Để phương trình có hai nghiệm dương thì \(\left\{{}\begin{matrix}-2\left(m-2\right)>0\\-2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)

Bài 1:
\(\Delta=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
=>-4m>-13
hay m<13/4
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=6\\2x_1-5x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x_2=14\\x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2\\x_1=1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-1\)
nên m-1=2
hay m=3
Bài 2:
\(\Delta=\left(2m-4\right)^2-4\cdot\left(-2m+1\right)\)
\(=4m^2-16m+16+8m-4\)
\(=4m^2-8m+12\)
\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Để phương trình có hai nghiệm dương thì \(\left\{{}\begin{matrix}-2\left(m-2\right)>0\\-2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)

1.
đk để pt có nghiệm \(\Delta\)>0 \(\Leftrightarrow\) (-3)2 -4(m-1) >0 \(\Leftrightarrow m< \dfrac{13}{4}\)
theo viet ta có :\(\left\{{}\begin{matrix}x_1+x_2=3\left(1\right)\\x_1\cdot_{ }x_2=m-1\left(2\right)\end{matrix}\right.\)
có 2x1-5x2=-8 (3)
kết hợp (1) , (3) :\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}5x_1+5x_2=15\\2x_1-5x_2=-8\end{matrix}\right.\)
cộng vế trên cho vế dưới :7x1=7\(\Rightarrow\)x1=1
có (1) : x1+x2=3 \(\Rightarrow\) x2=3-x1\(\Rightarrow\)x2=3-1=2
thay x1 và x2 vừa tìm đc vào (2) ta đươc \(1\cdot2=m-1\Leftrightarrow m=3\)(tm)
vậy m=3
2. đk để pt có 2 ng dương
\(\left\{{}\begin{matrix}\Delta'\ge0\\S>0\\P>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-2\right)^2-4\left(-2m+1\right)\ge0\\x_1+x_2=-2\left(m-2\right)>0\\x_1\cdot x_2=-2m+1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2\ge0\forall m\\m< 2\\m< \dfrac{1}{ }\end{matrix}\right.\)\(\Leftrightarrow m< \dfrac{1}{2}\) = 0,5
vậy m < 0,5

2/
Xét pt (1) có:
\(\Delta=4\left(m-2\right)^2-4.\left(-2m+1\right)\)
= \(4m^2-8m+12\)
= \(\left(2m-2\right)^2+8\)
Ta có: \(\left(2m-2\right)^2\ge0\) với mọi m
\(\Rightarrow\left(2m-2\right)^2+8>0\) với mọi m
\(\Rightarrow\) Phương trình luôn có 2 nghiệm phân biệt với mọi m
Áp ụng hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=4-2m\\x_1.x_2=1-2m\end{matrix}\right.\)
Để pt có 2 nghiệm dương \(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1.x_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4-2m>0\\1-2m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow m< \dfrac{1}{2}\)
Vậy với \(m< \dfrac{1}{2}\) thì pt đã cho có 2 nghiệm dương

Bài 1:
\(\Delta=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
=>-4m>-13
hay m<13/4
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=6\\2x_1-5x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x_2=14\\x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2\\x_1=1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-1\)
nên m-1=2
hay m=3
Bài 2:
\(\Delta=\left(2m-4\right)^2-4\cdot\left(-2m+1\right)\)
\(=4m^2-16m+16+8m-4\)
\(=4m^2-8m+12\)
\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Để phương trình có hai nghiệm dương thì \(\left\{{}\begin{matrix}-2\left(m-2\right)>0\\-2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)
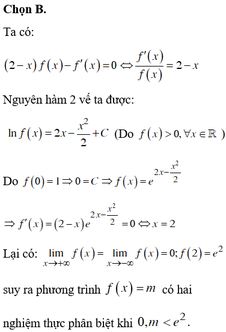
Chọn đáp án C
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Đặt ẩn phụ để giải phương trình: log 2 x = t . Tìm điều kiện để phương trình có nghiệm.
+) Dựa vào dữ kiện x 1 + x 2 = 6 tìm m. Từ đó tính x 1 - x 2 .
Phương trình đã cho có hai nghiệm phân biệt: x 1 , x 2 ⇔ phương trình (*) có hai nghiệm phân biệt ⇔ m ≠ 2 .