Cho tam giác DEF vuông tại D biết DE=3cm,DF=4cm.Kẻ đường trung tuyến DM (M€EF).Tính độ dài EF,DM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có ΔEDF cân ở D =>DE=DF; góc E =góc F
xét ΔDEM và ΔDFM có
DM là trung tuyến => EM=FM
góc E =góc F (cmt)
DE=DF (cmt)
=>ΔDEM = ΔDFM (cgc)
b)Có Δ DEF cân mà DM là trung tuyến
=> DM là đường cao (tc Δ cân )
=> DM⊥EF
c) EM=FM=EF/2=5
xét ΔDEM có DM ⊥ EF => góc EMD =90o
=>EM2+DM2=ED2 (đl pitago)
=>52+DM2=132 => DM=12
d) Ta có G là trọng tâm của ΔDEF
=>DG=2/3DM=> DG=2/3*12=8

Vì DM là trung tuyến ứng với cạnh huyền EF nên \(DM=\dfrac{1}{2}EF=\dfrac{5}{2}=2,5\left(cm\right)\)

a: ΔDEF vuông tại D
=>\(DE^2+DF^2+EF^2\)
=>\(EF^2=9^2+12^2=225\)
=>\(EF=\sqrt{225}=15\left(cm\right)\)
Ta có; ΔDEF vuông tại D
mà DM là đường trung tuyến
nên \(DM=\dfrac{EF}{2}=7,5\left(cm\right)\)
b: Xét tứ giác DNMK có
\(\widehat{DNM}=\widehat{DKM}=\widehat{KDN}=90^0\)
=>DNMK là hình chữ nhật
c: Xét ΔDEF có MN//DF
nên \(\dfrac{MN}{DF}=\dfrac{EM}{EF}\)
=>\(\dfrac{MN}{DF}=\dfrac{1}{2}\)
mà \(MN=\dfrac{1}{2}MH\)
nên MH=DF
Ta có: MN//DF
N\(\in\)MH
Do đó: MH//DF
Xét tứ giác DHMF có
MH//DF
MH=DF
Do đó: DHMF là hình bình hành
=>DM cắt HF tại trung điểm của mỗi đường
mà O là trung điểm của DM
nên O là trung điểm của HF
=>H,O,F thẳng hàng

a/ Xét tứ giác DPMQ có
∠EDF=∠MQD=ˆMPD=90oEDF^=MQD^=MPD^=90o
=> Tứ giác DPMQ là hcn
b/ Để hcn DPMQ là hình vuông thì DM là tia pg ^EDF
c/ Có I đx M qua DE
=> DE là đường t/trực của IM
=> DI = DM (1)
=> t/g DIM cân tại D có DE là đường trung trực
=> DE đồng thời là đường pg
=> ˆIDE=ˆEDMIDE^=EDM^ (2)
CMTT : DM = DK (3) ; ˆKDF=ˆFDMKDF^=FDM^ (4)
Từ (2) ; (4)
=> ∠IDE+∠EDF+∠KDF=∠IDK=180oIDE^+EDF^+KDF^=IDK^=180o
=> I,D,K thẳng hàng
Từ (1) ; (3)=> ID = DK
Do đó D là trđ IK
=> I đx K qua D

I là trung điểm của EF nên IE = IF = EF/2 = 5cm.
Ta có : 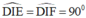 ⇒ ΔDIE vuông tại I
⇒ ΔDIE vuông tại I
Theo định lý Pitago trong tam giác vuông DIE ta có :
DE2 = DI2 + EI2 ⇒ DI2 = DE2 – EI2 = 132 – 52 = 144 ⇒ DI = 12 (cm).


a) Ta có: \(DE^2+DF^2=3^2+4^2=25\left(cm\right)\)
và \(EF^2=5^2=25\left(cm\right)\)
\(\Rightarrow DE^2+DF^2=EF^2\)
\(\Delta DEF\)có ba cạnh thỏa mãn định lý Py - ta - go nên \(\Delta DEF\) vuông
b) Vì DI là trung tuyến ứng với cạnh huyền của tam giác vuông \(DEF\)nên \(DI=\frac{1}{2}EF\)
\(\Rightarrow DI=\frac{1}{2}.5=2,5\left(cm\right)\)
c) Vì DI là trung tuyến ứng với cạnh huyền của tam giác vuông \(DEF\)nên \(DI=FI=EI\)
Lại có IK vuông góc DF
\(\Rightarrow\)IK là đường trung trực của đoạn thẳng DF
\(\Rightarrow IK=\frac{1}{2}DF=\frac{1}{2}.4=2\left(cm\right)\)

bài này tương tự bài 1
a) EF = 15
=> DM = EM = FM = 7,5
b) MND + D = 180
MND + 90 = 180
=> MND = 90
D + MED = 180
90 + MED = 180
=> MED = 90
=> DNME là hình chữ nhật
c) y hệt như bài trước mik giải

a) \(EF=\sqrt{3^2+4^2}=5\)(cm)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{3\cdot4}{5}=\dfrac{12}{5}=2,4\left(cm\right)\)
b) \(EF=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cm\right)\)
c) \(EF=\sqrt{12^2+5^2}=13\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\)
EF=căn 3^2+4^2=5cm
DM=5/2=2,5cm