Trên hình hai đường thẳng a và , b và c có song song không? c 120 120 160 80 A a B b C ...
Đọc tiếp
Trên hình hai đường thẳng a và , b và c có song song không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 6 2017
Chọn (D) hai cung chứa góc 120° (đối xứng nhau) dựng trên hai điểm A, B).
HC
31 tháng 8 2020
Bài giải
a, Nếu \(\widehat{A_1}=120^o\text{ ; }\widehat{B_3}=130^o\text{ }\text{thì }a\text{ không song song }b\)
Muốn \(a\text{ }//\text{ }b\text{ thì }\orbr{\begin{cases}\widehat{A_1}=\widehat{B_3}=130^o\\\widehat{A_1}=\widehat{B_3}=120^o\end{cases}}\) để hai góc bằng nhau ( so le ngoài )
b, Nếu \(\widehat{A_2}=65^o\text{ ; }\widehat{B_3}=64^o\) thì a không song song b
Muốn \(a\text{ }//\text{ }b\text{ thì }\orbr{\begin{cases}\widehat{A}_2=\widehat{B_3}=65^o\\\widehat{A_2}=\widehat{B_3}=64^o\end{cases}}\) để hai góc bằng nhau
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
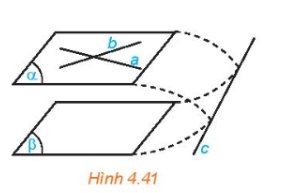
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
5 tháng 10 2021
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
18 tháng 9 2023
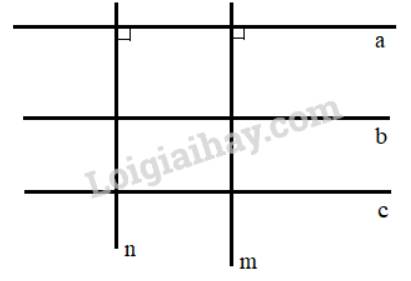
Ta có: +) a // b, b // c nên a // c ( Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)
+) m \( \bot \) a; n \( \bot \)a nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia, ta có:
+) a // b; a \( \bot \)n nên b \( \bot \)n
+) a // b; a \( \bot \)m nên b \( \bot \)m
+) a // c; a \( \bot \)n nên c \( \bot \)n
+) a // c; a \( \bot \)m nên c \( \bot \)m
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
Các cặp đường thẳng vuôn góc là: b \( \bot \)n; b \( \bot \)m; c \( \bot \)n; c \( \bot \)m; a \( \bot \)n; a \( \bot \)m
A B C không song song với nhau