Cho tam giác XYZ vuông tại X. Trên tia XZ lấy điểm A và vẽ đường tròn có đường kính AZ. Kẻ YA cắt đường tròn tại B. Đường thẳng BX cắt đường tròn tại C a, Chứng minh 4 điểm X,Y,Z,B cùng thuộc 1 đường tròn b, Chứng minh góc XYB bằng góc XZB c, XZ là tia phân giác của góc CZY
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2021
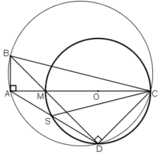
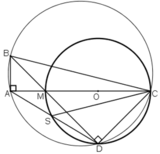
a: Xét tứ giác OBMC có
\(\widehat{OBM}+\widehat{OCM}=180^0\)
Do đó: OBMC là tứ giác nội tiếp
CM
17 tháng 5 2017
+ Trong đường tròn đường kính MC:
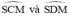đều là các góc nội tiếp cùng chắn cung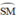 
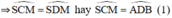
+ Trong đường tròn đường kính BC:
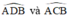đều là các góc nội tiếp chắn cung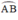 
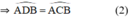
30 tháng 12 2018
a, Vì CM là tiếp tuyến của (A)
=> \(CM\perp AM\)
=> ^CMA = 90o
=> M thuộc đường tròn đường kính AC
Vì ^CHA = 90o
=> H thuộc đường tròn đường kính AC
Do đó : M và H cùng thuộc đường tròn đường kính AC
hay 4 điểm A,C,M,H cùng thuộc đường tròn đường kính AC
b, Vì AM = AH ( Bán kính)
CM = CH (tiếp tuyến)
=> AC là trung trực MH
=> \(AC\perp MH\)tại I
Xét \(\Delta\)AMC vuông tại M có MI là đường cao
\(\Rightarrow MA^2=AI.AC\)(Hệ thức lượng)
c, Vì CM , CH là tiếp tuyến của (A)
=> AC là phân giác ^HAM
=> ^HAC = ^MAC
Mà ^HAC + ^HAB = 90o
=> ^MAC + ^HAB = 90o
Ta có: ^BAD + ^BAC + ^CAM = 180o (Kề bù)
=> ^BAD + 90o + ^CAM = 180o
=> ^BAD + ^CAM = 90o
Do đó ^BAD = ^BAH (Cùng phụ ^CAM)
Xét \(\Delta\)BAD và \(\Delta\)BAH có:
AB chung
^BAD = ^BAH (cmt)
AD = AH (Bán kính (A) )
=> \(\Delta BAD=\Delta BAH\left(c.g.c\right)\)
=> ^ADB = ^AHB = 90o
\(\Rightarrow BD\perp AD\)
=> BD là tiếp tuyến của (A)
Làm đc đến đây thôi :(
CM
19 tháng 11 2019
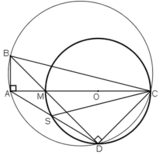
a)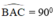 
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
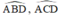đều là góc nội tiếp chắn cung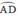 
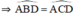
c) + Trong đường tròn đường kính MC:
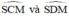đều là các góc nội tiếp cùng chắn cung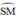 
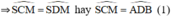
+ Trong đường tròn đường kính BC:
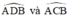đều là các góc nội tiếp chắn cung 
26 tháng 2 2023
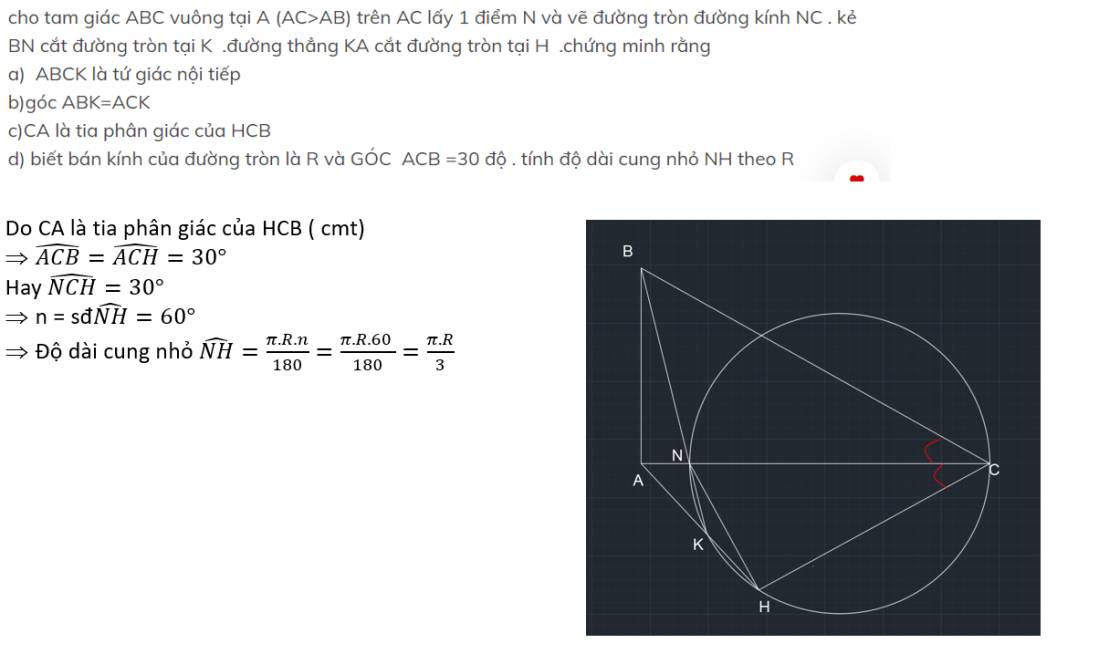
a: Xét (O) có
ΔCKN nội tiếp
CN là đường kính
=>ΔCKN vuông tại K
Xét tứ giác ABCK co
góc CKB=góc CAB=90 độ
=>ABCK là tứ giác nội tiếp
b: ABCK là tứ giác nội tiếp
=>góc ABK=góc ACK
c: ABCK là tư giác nội tiếp
=>góc ACB=góc AKB
mà góc AKB=góc HCA
nên góc HCA=góc BCA
=>CA làphân giác của góc HCB
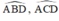đều là góc nội tiếp chắn cung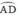 
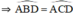
a) Xét (O) có
\(\widehat{ZBA}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ZBA}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{ZBY}=90^0\)
Xét tứ giác XYZB có
\(\widehat{ZBY}=\widehat{ZXY}\left(=90^0\right)\)
\(\widehat{ZBY}\) và \(\widehat{ZXY}\) là hai góc đối
Do đó: XYZB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)