Cho hình thang ABCD có đáy nhỏ AB= 3cm. Gọi N;I là trung điểm các đường chéo. Biết độ dài đường trung bình bằng 5. Khi đó độ dài của NI là .................... cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dễ dàng chứng minh được N,I cùng nằm trên đường trung bình của hình thang (Có thể chứng minh theo tiên đề Ơ-clit)
Khi đó ta có \(NP=IQ=\frac{1}{2}AB=\frac{3}{2}\left(cm\right)\)
NI = PQ - 2NP = 5-3 = 2 (cm)
Chỉ làm r: Câu hỏi của ༺ ๖ۣۜPhạm ✌Tuấn ✌Kiệτ ༻ - Toán lớp 8 | Học trực tuyến

Vì tứ giác ABCD là hình thang cân (gt).
=> AD = BC (Tính chất hình thang cân).
Mà BC = 2 (cm).
=> AD = 2 (cm).
Chu vi hình thang ABCD là:
AB + CD + BC + AD = 3 + 5 + 2 + 2 = 12 (cm).
p hình thang cân là :
3 + 5 + 2 + 2 = 12 cm
Đ/S : 12 cm

Đáp án cần chọn là: A.
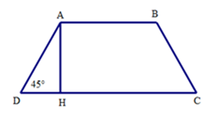
Ta có tam giác ADH vuông cân tại H vì D ^ = 45 ° .
Do đó DH = AH = 5cm
Mà DH = 1 2 (CD – AB)
Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)
Vậy CD = 13 cm
NI=2cm