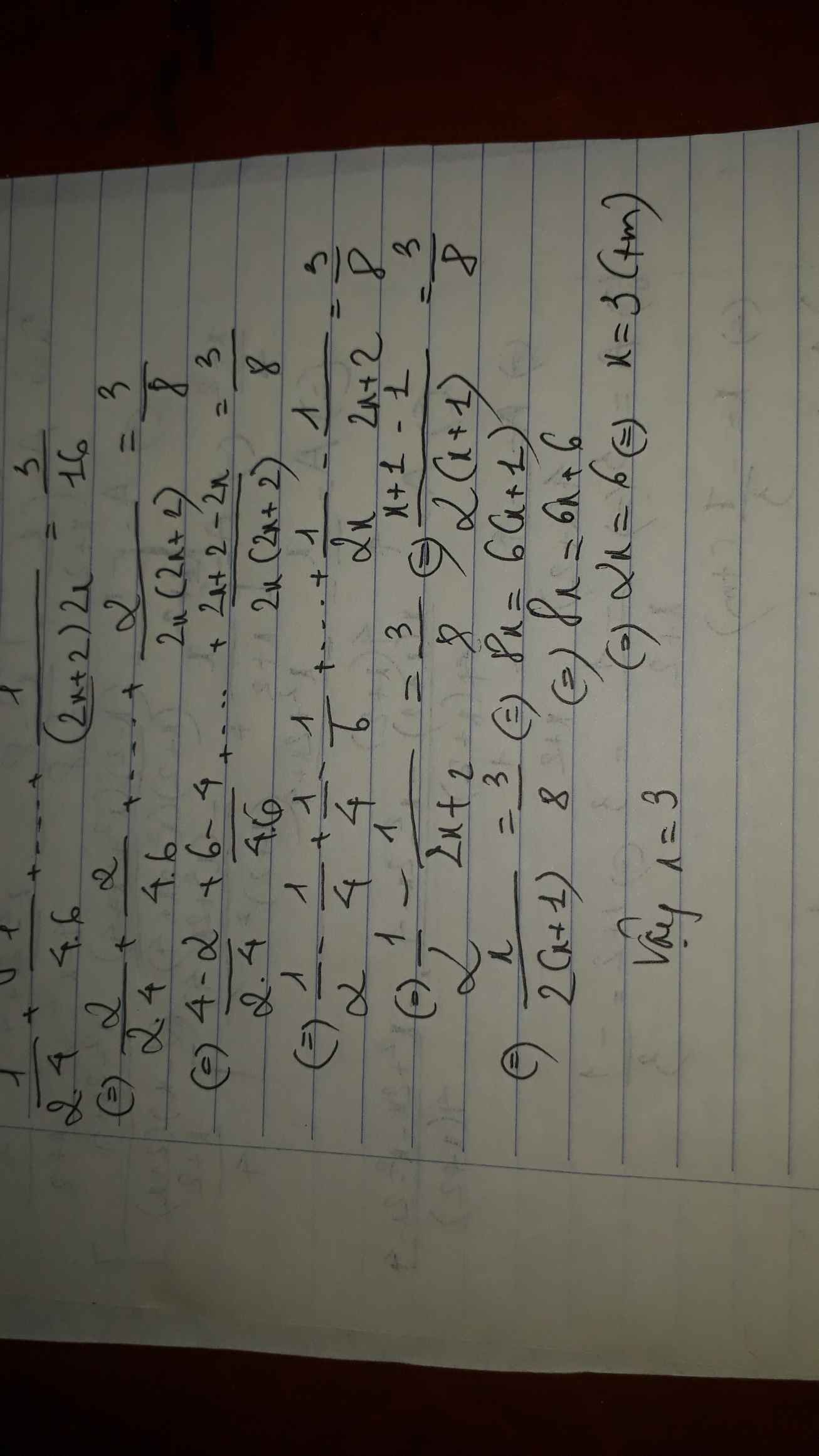1/2x4+1/4x6+…+1/(2x-2)x 2x=3/16 (x thuộc N , x lớn hơn hoặc bằng 2) Cíu mình zứi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MK
1
NM
3
15 tháng 10 2021
\(S=8+8^3+...+8^{2x+1}\\ \Rightarrow64S=8^3+8^5+...+8^{2x+3}\\ \Rightarrow64S-S=\left(8^3+8^5+...+8^{2x+3}\right)-\left(8+8^3+...+8^{2x+1}\right)\\ \Rightarrow63S=8^{2x+3}-8\\ \Rightarrow S=\dfrac{8^{2x+3}-8}{63}\)
9 tháng 9 2021
\(1,x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\\ 2,-2x^2-x-1=-2\left(x^2+2\cdot\dfrac{1}{4}x+\dfrac{1}{16}+\dfrac{7}{16}\right)\\ =-2\left(x+\dfrac{1}{4}\right)^2-\dfrac{7}{8}\le-\dfrac{7}{8}< 0\\ 3,\dfrac{1}{2}x^2-2x+2=\dfrac{1}{2}\left(x^2-4x+4\right)=\dfrac{1}{2}\left(x-2\right)^2\ge0\)
16 tháng 6 2023
b: =>(x-4)(x-3)(x-1)>0
=>1<x<3 hoặc x>4
c: =>(2x-1)(x-1)(2x-3)<0
=>x<1/2 hoặc 1<x<3/2
VH
15 tháng 7 2019
1) Đề sai, thử với x = -2 là thấy không thỏa mãn.
Giả sử cho rằng với đề là x không âm thì áp dụng BĐT Cauchy:
\(A=\)\(\frac{2x}{3}+\frac{9}{\left(x-3\right)^2}=\frac{x-3}{3}+\frac{x-3}{3}+\frac{9}{\left(x-3\right)^2}+2\)
\(A\ge3\sqrt[3]{\frac{\left(x-3\right).\left(x-3\right).9}{3.3.\left(x-3\right)^2}}+2=3+2=5>1\)
Không thể xảy ra dấu đẳng thức.
10 tháng 7 2022
a: 2x+1<=6
=>2x<=5
=>x<=5/2
=>A={0;1;2}
b: B={1;5}
c: \(C=\varnothing\)
d: D={0;2;4;6}
15 tháng 11 2018
1) \(\left(x-1\right)\left(x+2\right)< 0\Leftrightarrow-2< x< 1\)
vậy \(x=-1;0\)
2) \(\left(x+1\right)\left(2x-4\right)\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le-1\end{matrix}\right.\)
vậy \(x=Z\backslash\left\{1;0\right\}\)
3) \(\left(x^2+1\right)\left(x^2-4\right)\le0\)
vì \(x^2+1\ne0\)
\(\Leftrightarrow x^2-4\le0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\le0\Leftrightarrow-2\le x\le2\)
vậy \(x=-2;-1;0;1;2\)
4) \(\left|x\right|\left(x^2-1\right)\ge0\)
ta có \(\left|x\right|\ge0\)
\(\Leftrightarrow x^2-1\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\x\le-1\end{matrix}\right.\)
vậy \(x=Z\backslash\left\{0\right\}\)
17 tháng 6 2022
1: (x-1)(x+2)<0
=>-2<x<1
mà x là số nguyên
nên \(x\in\left\{-1;0\right\}\)
2: \(\left(x+1\right)\cdot\left(2x-4\right)>=0\)
=>x>=2 hoặc x<=-1
mà x là số nguyên
nên x=Z\{1;0}
3: \(\Leftrightarrow x^2-4< =0\)
=>-2<=x<=2
mà x là số nguyên
nên \(x\in\left\{-2;-1;0;1;2\right\}\)
4: =>(x2-1)>=0
=>x>=1 hoặc x<=-1
=>x=Z\{0}