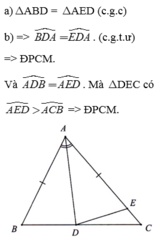
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Trên AC lấy E sao cho AE AB. CMR: Tam giác BDE là tam giác cân?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tự vẽ hình nha !
Xét tam giác ABD và tam giác AED có :
AB = AE ( giả thiết )
Góc BAD = góc EAD ( vì AD là tia phân giác góc BAC )
Cạnh AD chung
Suy ra tam giác ABD = tam giác AED ( c-g-c )
Do đó BD = DE ( 2 cạnh tương ứng ) hay tam giác BDE cân tại D
Vậy tam giác BDE cân tại D

a) Xét hai tg ABD và AED có: AE = AB (gt)
góc BAD = góc EAD
AD chung
DO đó tg ADB = tg AED (c.g.c)
=> BD = DE
=> tam giác BDE cân tại D (đcpm)

a) Xét \(\Delta\)BAE và \(\Delta\)DAC có: ^BAE = ^DAC ( đối đỉnh ) ; AD = AB ( gt ) ; AE = AC ( gt )
=> \(\Delta\)BAE = \(\Delta\)DAC ( c.g.c)
=> BE = DC
b) Tương tự câu a dễ dàng cm đc: \(\Delta\)ADE = \(\Delta\)ABC => ^ADE = ^ABC => DE//BC
=> ^EDI = ^DIC mà ^EDI = ^BDI ( DI là phân giác ^BDE )
=> ^DIC = ^BDI hay ^DIB = ^IDB => \(\Delta\)BDI cân tại B.
c) Ta có: ^DBC là góc ngoài tại đỉnh B của \(\Delta\)BDI => ^DBC = ^BDI + ^BID = 2. ^BID = 2. ^CIF( theo b) (1)
Có: CF là phân giác ^BCA =>^BCF = ^ACF => ^BCA = ^BCF + ^ACF = 2. ^BCF = 2. ^ICF (2)
Lại có: ^CFD là góc ngoài của \(\Delta\)FCI => ^CFD = ^CIF + ^ICF (3)
Từ (1) ; (2) ; (3) => 2 .^CFD = 2 ^CIF + 2. ^ICF = ^DBC + ^BCA = ^DBC + ^CED ( ^CED = ^BCA vì ED //BC )