chứng minh công thứ
a) ( a. b )n = an. bm
b) ( a: b ) m = a m ; b m
c) ( a m ) n = am . n
nâng cao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 11 2017
a)Tam giác MAK =tgKCB(c.g.c) (1) ->AM=BC (2 cạnh tương ứng ) b) tg ANE=tg EBC (c.g.c) (2) ->AN=BC (2 cạnh tương ứng) c) vì AN =BC , AM=BC ->AN=AM
d) từ (1) suy ra góc AMK =góc KCB (2 góc t ứng )
Mà chúng ở vị trí so le trong suy ra AM//BC
e) từ (2) -> góc ANE =góc EBC (2 góc t ứng ) mà chúng ở vị trí so le trong -> AN//BC
g) vì AN//BC , AM//BC -> A,N,N thẳng hàng (3)
Mà MA= BC , AN =BC
-> MA=AN (4)
Từ (3) , (4) -> A là trung điểm của MN
10 tháng 10 2021
Xét ΔCEB có
F là trung điểm của CE
M là trung điểm của BC
Do đó: FM là đường trung bình của ΔCEB
Suy ra: FM//EN
Xét ΔAMF có
E là trung điểm của AF
EN//FM
Do đó: N là trung điểm của AM
hay \(\overrightarrow{AN}+\overrightarrow{MN}=\overrightarrow{0}\)
CM
3 tháng 9 2017
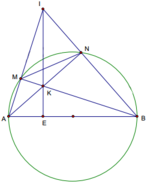
a. Ta thấy AN^ BI ,BM ^AI , nên K là trực tâm tam giác IAB. Do đó IK^ AB
b. Vì DAEK∽ DANB ∽ nên AK. AN =AE .AB
Tương tự vì DBEK∽ DBMA ∽ nên BK .BM =BE. BA
Vậy AK.AN+BK.BM=AE.AB+BE.BA=AB2
25 tháng 2 2023
a: Vì OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB=2cm
OM=OA/2=2cm<OA
=>M nằm giữa O và B
=>OM+MB=OB
=>MB=4cm
b: Vì BA=1/2BM
nên A là trung điểm của BM
2 tháng 4 2023
a: Xét ΔBAM và ΔBNM có
BA=BN
góc ABM=góc NBM
BM chung
=>ΔBAM=ΔBNM
b: ΔBAN cân tại B
mà BI là phân giác
nên I là trung điểm của AN
c: góc NMC+góc AMN=180 độ
góc AMN+góc ABC=180 độ
=>góc NMC=góc ABC
16 tháng 11 2018
Hôm nay sáng mồng hai tháng chín
Thủ đô hoa vàng nắng Ba Đình
Muôn triệu tim chờ chim vẫn nín
Bỗng vang lên tiếng hát ân tình
Hồ Chí Minh, Hồ Chí Minh
Người đứng trên đài lặng phút giây
Trông đàn con đó vẫy hai tay
Cao cao vầng trán ngời đôi mắt
Độc lập bây giờ mới thấy đây.
9 tháng 11 2021
a, Xét \(\Delta ABM\) và \(\Delta ACM\) có \(\left\{{}\begin{matrix}AB=AC\\\widehat{BAM}=\widehat{CAM}\left(AM.là.p/g\right)\\AM.chung\end{matrix}\right.\)
Do đó \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
\(\Rightarrow CM=BM\)
b, Xét \(\Delta ABI\) và \(\Delta ACI\) có \(\left\{{}\begin{matrix}AB=AC\\\widehat{BAM}=\widehat{CAM}\left(AM.là.p/g\right)\\AI.chung\end{matrix}\right.\)
Do đó \(\Delta ABI=\Delta ACI\left(c.g.c\right)\)
\(\Rightarrow\widehat{AIB}=\widehat{AIC}\)
Mà \(\widehat{AIB}+\widehat{AIC}=180^0\) (kề bù) nên \(\widehat{AIB}=\widehat{AIC}=90^0\)
Do đó AI⊥BC
Mà DH⊥BC nên AI//DH
Do đó \(\widehat{BDH}=\widehat{BAI}\) (đồng vị)
Mà \(2\widehat{BAI}=\widehat{A}\) (AM là phân giác, AM trùng AI)
Vậy \(\widehat{A}=2\widehat{BDH}\)