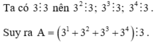chứng minh rằng:30+32+34+....+32002chia hết cho 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
1
31 tháng 10 2021
b: \(S=\left(3^0+3^2+3^4\right)+...+3^{1998}\left(3^0+3^2+3^4\right)\)
\(=91\cdot\left(1+...+3^{1998}\right)⋮7\)
LK
1
11 tháng 10 2021
b: \(S=3^0+3^2+3^4+...+3^{2002}\)
\(=\left(3^0+3^2+3^4\right)+...+3^{1998}\left(3^0+3^2+3^4\right)\)
\(=91\cdot\left(1+...+3^{1998}\right)⋮7\)
ND
1
AH
Akai Haruma
Giáo viên
29 tháng 1 2023
Lời giải:
a.
$S=3^0+3^2+3^4+...+3^{2002}$
$3^2S=3^2+3^4+3^6+...+3^{2004}$
$3^2S-S=(3^2+3^4+3^6+...+3^{2004})-(3^0+3^2+3^4+...+3^{2002})$
$8S=3^{2004}-3^0=3^{2004}-1$
$S=\frac{3^{2004}-1}{8}$
b.
$S=(3^0+3^2+3^4)+(3^6+3^8+3^{10})+....+(3^{1998}+3^{2000}+3^{2002})$
$=(3^0+3^2+3^4)+3^6(3^0+3^2+3^4)+....+3^{1998}(3^0+3^2+3^4)$
$=(3^0+3^2+3^4)(1+3^6+...+3^{1998})$
$=91(1+3^6+...+3^{1998})=7.13(1+3^6+...+3^{1998})\vdots 7$
Ta có đpcm.
TN
1
23 tháng 8 2023
= ( 72024 + 32 ). ( 71012 . 71012 + 34 )
= ( 72024 + 32 ) . ( 72024 + 34 )
= 72024 ( 32 + 34 )
= 72024 . 66 ⋮ 6
KV
23 tháng 12 2023
A = 8⁸ + 2²⁰
= (2³)⁸ + 2²⁰
= 2²⁴ + 2²⁰
= 2²⁰.(2⁴ + 1)
= 2²⁰.17 ⋮ 17
Vậy A ⋮ 17
TT
1
8 tháng 11 2023
`#3107.101107`
\(A=1+3+3^2+3^3+...+3^{101}\)
$A = (1 + 3 + 3^2) + (3^3 + 3^4 + 3^5) + ... + (3^{99} + 3^{100} + 3^{101}$
$A = (1 + 3 + 3^2) + 3^3 (1 + 3 + 3^2) + ... + 3^{99}(1 + 3 + 3^2)$
$A = (1 + 3 + 3^2)(1 + 3^3 + ... + 3^{99})$
$A = 13(1 + 3^3 + ... + 3^{99})$
Vì `13(1 + 3^3 + ... + 3^{99}) \vdots 13`
`\Rightarrow A \vdots 13`
Vậy, `A \vdots 13.`
T
8 tháng 11 2023
\(A=1+3+3^2+3^3+3^4+3^5+...+3^{101}\\=(1+3+3^2)+(3^3+3^4+3^5)+(3^6+3^7+3^8)+...+(3^{99}+3^{100}+3^{101})\\=13+3^3\cdot(1+3+3^2)+3^6\cdot(1+3+3^2)+...+3^{99}\cdot(1+3+3^2)\\=13+3^3\cdot13+3^6\cdot13+...+3^{99}\cdot13\\=13\cdot(1+3^3+3^6+...+3^{99})\)
Vì \(13\cdot(1+3^3+3^6...+3^{99}\vdots13\)
nên \(A\vdots13\)
\(\text{#}Toru\)
HT
1
16 tháng 12 2021
\(A=1+3+3^2+3^3+...+3^{102}+3^{103}\)
\(\Rightarrow A=\left(1+3\right)+\left(3^2+3^3\right)+...+\left(3^{102}+3^{103}\right)\)
\(\Rightarrow A=\left(1+3\right)+3^2\left(1+3\right)+...+3^{102}\left(1+3\right)\)
\(\Rightarrow A=\left(1+3\right)\left(1+3^2+...+3^{102}\right)\)
\(\Rightarrow A=4\left(1+3^2+...+3^{102}\right)⋮4\)
MY
2
PT
1
