Phân tích đa thức thành nhân tử
\(^{x^2-5x+6}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
RV
3
Những câu hỏi liên quan
2 tháng 11 2018
x2 - 5x + 6
= x2 - 2x - 3x + 6
= ( x2 - 2x ) - ( 3x - 6 )
= x( x - 2 ) - 3( x - 2 )
= ( x - 3 )( x - 2 )
1 tháng 6 2019
Ta có: x2 + 5x - 6
= x2 + 6x - x - 6
= x(x + 6) - (x + 6)
= (x - 1)(x + 6)
1 tháng 6 2019
\(x^2+5x-6\)
\(=x^2+6x-x-6\)
\(=x.\left(x+6\right)-\left(x+6\right)\)
\(=\left(x-1\right)\left(x+6\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 12 2021
\(4x^2-5x-6=4x^2-8x+3x-6\)
\(=4x\left(x-2\right)+3\left(x-2\right)\)
\(=\left(x-2\right)\left(4x+3\right)\)
PT
1
CM
24 tháng 9 2019
Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.
a) x2 – 3x + 2
= x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2)
= x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2
= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6
= (x2 – 22) – 3(x – 2)
= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)
b) x2 + x – 6
= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c) x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)
a) x2 – 3x + 2
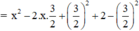
(Vì có x2 và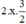 
nên ta thêm bớt 
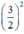để xuất hiện HĐT)
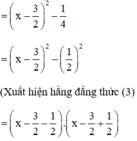
= (x – 2)(x – 1)
b) x2 + x - 6
= (x – 2)(x + 3).
c) x2 + 5x + 6
= (x + 2)(x + 3).
QB
0
DA
3
31 tháng 7 2021
e ko bt phân tích đa thức thành nhân tử nên a tham khảo linh này nha
https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwim29i-oIzyAhVSNKYKHZBdCJ4QFjAAegQIBRAD&url=https%3A%2F%2Fh7.net%2Fhoi-dap%2Ftoan-8%2Fphan-h-da-thuc-5x-2-2x-2-2x-5x-2-6-thanh-nhan-tu-faq341450.html&usg=AOvVaw2Kkix8idzI43uM1i2Mitp4
KG
0
\(x^2-5x+6\)
\(=x^2-5x+\frac{25}{4}-\frac{1}{4}\)
\(=\left(x-\frac{5}{2}\right)^2-\left(\frac{1}{2}\right)^2\)
\(=\left(x-\frac{5}{2}-\frac{1}{2}\right)\left(x-\frac{5}{2}+\frac{1}{2}\right)\)
\(=\left(x-3\right)\left(x-2\right)\)
\(x^2-5x+6 \)
= \(x^2-2x-3x+6\)
= \(\left(x^2-2x\right)-\left(3x-6\right)\)
= \(x\left(x-2\right)-3\left(x-2\right)\)
= \(\left(x-2\right)\left(x-3\right)\)