\(\frac{1}{2}\)- 0, 03 =
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Học sinh thực hành.
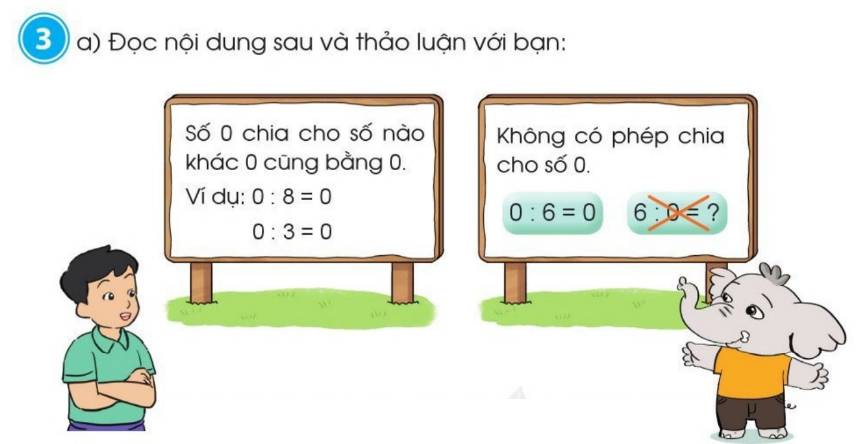
b)
0 : 7 = 0 0 : 9 = 0 | 0 : 5 = 0 0 : 4 = 0 | 0 : 10 = 0 0 : 1 = 0 |
c) Các phép tính sai là:
8 : 1 = 1. Sửa: 8 : 1 = 8.
2 : 0 = 0. Sửa: 0 : 2 = 0.
3 : 0 = 0. Sửa: 0 : 3 = 0.

1. x(x + 1) - x2 + 1 = 0
<=> x(x + 1) - (x2 - 1) = 0
<=> x(x + 1) - (x + 1)(x - 1) = 0
<=> (x - x + 1)(x + 1) = 0
<=> x + 1 = 0\
<=> x = -1
2. 4x(x - 2) - 6 + 3x = 0
<=> 4x(x - 2) - (3x - 6) = 0
<=> 4x(x - 2) - 3(x - 2) = 0
<=> (4x - 3)(x - 2) = 0
<=> \(\left[{}\begin{matrix}4x-3=0\\x-2=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=2\end{matrix}\right.\)
3. x(x + 2) - 3(x + 2) = 0
<=> (x - 3)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x-3=0\\x+2=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

\(3x^4+x^2-4=0\)
\(\Leftrightarrow3x^4-3x^2+4x^2-4=0\)
\(\Leftrightarrow3x^2\cdot\left(x^2-1\right)+4\cdot\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(3x^2+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=0\\3x^2+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm1\\x^2=-\dfrac{4}{3}\left(l\right)\end{matrix}\right.\)
\(S=\left\{\pm1\right\}\)
Đặt `x^2=t(t>=0)`
Ta có PT: `3t^2+t-4=0`
`3+1-4=0`
`=> t_1 = 1 ; t_2 = -4/3 (L)`
`=> x^2=1`
`<=> x=\pm 1`
Vậy `S={\pm 1}`.
1) cosx\(^2\)+sinx=0
2) 2cos\(^2\)x-cos2x+cosx=0
3) sin\(^2\)x-3cos2x-2=0
4) tanx+\(\dfrac{2}{cotx}\)=0

3.
\(\dfrac{1}{2}-\dfrac{1}{2}cos2x-3cos2x-2=0\)
\(\Leftrightarrow-7cos2x-3=0\)
\(\Rightarrow cos2x=-\dfrac{3}{7}\)
\(\Rightarrow2x=\pm arccos\left(-\dfrac{3}{7}\right)+k2\pi\)
\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(-\dfrac{3}{7}\right)+k\pi\)
4.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(tanx+2tanx=0\)
\(\Rightarrow3tanx=0\)
\(\Rightarrow tanx=0\)
\(\Rightarrow x=k\pi\) (loại do ĐKXĐ)
Vậy pt đã cho vô nghiệm
1.
\(\Leftrightarrow1-sin^2x+sinx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{5}}{2}>1\left(loại\right)\\sinx=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\) (\(k\in Z\))
2.
\(2cos^2x-\left(2cos^2x-1\right)+cosx=0\)
\(\Leftrightarrow cosx+1=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\) (\(k\in Z\))
 một khối gỗ có dạng hình hộp chữ nhật được cắt đi 1 phần như hình vẽ. tính thể tích của phần bị cắt
một khối gỗ có dạng hình hộp chữ nhật được cắt đi 1 phần như hình vẽ. tính thể tích của phần bị cắt
\(\frac{1}{2}-0,03=0,47=\frac{47}{100}\)
nha bn
đúng k
\(\frac{1}{2}-0,03\)
= 0,5 - 0,03
= 0,47