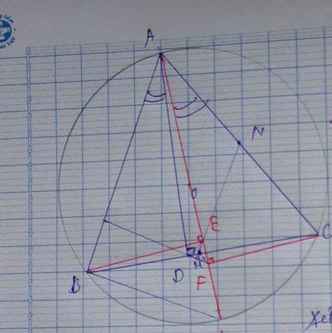
cho tam giác 1bc nhọn nội tiếp đường tròn tâm O. Kẻ đường cao AD của tam giác ABC , đường kính AKcuar đường tròn tâm O . Gọi E và F lần lượt là hình chiếu của
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 2 2022
Tết nghỉ ngơi đi em, thời gian này nên chơi cho đầu óc thanh thản chứ ko nên học
Hướng dẫn sơ sơ cách giải cho câu này:
Trước hết em chứng minh \(MN\perp DF\)
Sau đó chứng minh \(DN=NF\) (đều bằng \(\dfrac{1}{2}AC\), lý do là 2 trung tuyến của 2 tam giác vuông đều có cạnh huyền AC)
\(\Rightarrow MN\) là trung trực DF (1)
Hoàn toàn tương tự, gọi P là trung điểm AB thì cũng chứng minh được \(MP\perp DE\) và \(PD=PE\Rightarrow PM\) là trung trực DE (2)
(1);(2) suy ra đpcm
MN
2 tháng 2 2022
Tham khảo :
Cái này mình tham khảo ở Qanda nha ko đúng đc thì thui bạn nha :
DT
2 tháng 2 2022
MN vuông góc DF
=>EM vuông góc DF
AK là đường kính , BC là đây cung (1)
=> AK vuông góc BC hay DM vuông góc DF(2)
Từ (1) và (2) suy ra:
M là tâm đường tròn ngoại tiếp tam giác DEF
CH
Cô Hoàng Huyền
Admin
VIP
9 tháng 2 2018
+ ) Ta thấy ngay hai tam giác vuông AHC và ANC có chung cạnh huyền AC nên A, H, N, C cùng thuộc đường tròn đường kính AC.
\(\Rightarrow\widehat{HNA}=\widehat{HCA}\) (Hai góc nội tiếp cùng chắn cung AH)
Ta thấy ngay hai tam giác vuông AMB và AHB có chung cạnh huyền AB nên A, M, H, B cùng thuộc đường tròn đường kính AB.
\(\Rightarrow\widehat{HMN}=\widehat{ABH}\) (Góc ngoài tại đỉnh đối diện bằng góc trong tại đỉnh)
Vậy nên \(\Delta ABC\sim\Delta HMN\left(g-g\right)\)
+) Ta có \(\widehat{ADC}=\widehat{ABC}\) (Hai góc nội tiếp cùng chắn cung AC)
Mà \(\Delta ABC\sim\Delta HMN\Rightarrow\widehat{ABC}=\widehat{HMN}\)
nên \(\widehat{ADC}=\widehat{HMN}\)
Chúng lại ở vị trí so le trong nên DC // HM
Ta có \(DC\perp AC\Rightarrow HM\perp AC\)
Gọi J là trung điểm AB
Ta có ngay IJ là đường trung bình tam giác ABC nên IJ // AC
Vậy nên \(HM\perp IJ\)
Mà J là tâm đường tròn ngoại tiếp tứ giác AMHB nên IJ vuông góc cung HM tại trung điểm HM hay IJ là trung trực của HM.
Vậy thì IM = IH.
Tương tự ta có IM = IH = IN hay I là tâm đường tròn ngoại tiếp tam giác HMN.