GIÚP EM CÂU C BÀI 1 VỚI Ạ,EM CÁM ƠN Ạ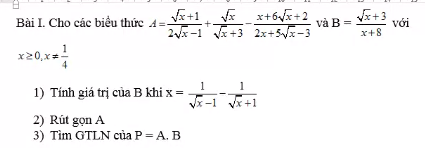
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.

Hello! John.
Glad to see you again. Tam, this is my cousin, Peter. It's his first to visit to your country.
How do you do? Welcome to VN
Thank you. Nice to meet you, Tam
Can I help you with your suitcases, John?
Thanks. I can manage.
OK. Now we're going to the hotel in the center of the city by taxi
That would be nice. How far is it from the airport to the center of the city?
It's about a half-hour drive
Look, John! What a lot of motorbikes in the streets!
Oh, yeah. That surprised me by the time I first came to VN
Motorbikes are our main means of transport. I go to school every day by bike.
Would you mind taking me around the city by bike?
No, of course not. But I have to ask someone else to get Peter, too
Peter, do you mind if Tam's friend gives us a ride around the city?
No, I don't mind. But I feel a little bit scared because the traffic is so heavy
OK. So we'll go on a sightseeing tour by bikes at weekend

Câu 4:
4.1/ Ta có: \(n_{NaCl}=2,5.0,4=1\left(mol\right)\)
\(\Rightarrow m_{NaCl}=1.58,5=58,5\left(g\right)\)
4.2/ Ta có: \(n_{Zn}=\dfrac{13}{65}=0,2\left(mol\right)\)
a, PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\)
_____0,2___________0,2____0,2 (mol)
b, \(V_{H_2}=0,2.22,4=4,48\left(l\right)\)
c, \(m_{ZnCl_2}=0,2.136=27,2\left(g\right)\)
Bạn tham khảo nhé!

a) Xét ΔMNI vuông tại M và ΔHPI vuông tại P có
\(\widehat{MIN}=\widehat{HIP}\)(hai góc đối đỉnh)
Do đó: ΔMNI\(\sim\)ΔHPI(g-g)
b) Ta có: ΔMNI\(\sim\)ΔHPI(cmt)
nên \(\widehat{MNI}=\widehat{HPI}\)(hai góc tương ứng)
hay \(\widehat{MNI}=\widehat{MPK}\)
Xét ΔMNI vuông tại M và ΔMPK vuông tại M có
\(\widehat{MNI}=\widehat{MPK}\)(cmt)
Do đó: ΔMNI\(\sim\)ΔMPK(g-g)
Suy ra: \(\dfrac{MN}{MP}=\dfrac{MI}{MK}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)
Xét ΔMNP vuông tại M và ΔMIK vuông tại M có
\(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)(cmt)
Do đó: ΔMNP\(\sim\)ΔMIK(c-g-c)

\(f\left(1-3x\right)=2\left(1-3x\right)-\left(1-3x\right)^2=1-9x^2\)


a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE và AC=BE
b: Xét tứ giác AIEK có
AI//KE
AI=KE
Do đó: AIEK là hình bình hành
Suy ra: Hai đường chéo AE và IK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AE
nên M là trung điểm của IK
hay I.M,K thẳng hàng

\(\dfrac{2020}{2019}>\dfrac{2019}{2020}\Rightarrow0< a< 1\)
\(log_ba< 1\Rightarrow b>1\)
\(P=log_b^2a+log_b^22-\dfrac{m^2log_2b}{log_2a}+2\left(log_ba-2log_b2\right)-\dfrac{4^{ab^2}-2m.2^{ab^2}}{log_ba}\)
\(=log_b^2a+log_b^22+2log_ba-4log_b2-\dfrac{4^{ab^2}-2m.2^{ab^2}+m^2}{log_ba}\)
\(=\left(log_ba+1\right)^2+\left(log_b2-2\right)^2+\dfrac{\left(2^{ab^2}-m\right)^2}{-log_ba}-5\ge-5\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}log_ba=-1\\log_b2=2\\2^{ab^2}=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{2}}\\b=\sqrt{2}\\m=2^{ab^2}=2^{\sqrt{2}}\end{matrix}\right.\)
Sau khi tính lại thì không có đáp án nào đúng :(

a)\(R_{23}=R_2+R_3=2+4=6\Omega\)
\(R_{123}=\dfrac{R_1\cdot R_{23}}{R_1+R_{23}}=\dfrac{2\cdot6}{2+6}=1,5\Omega\)
\(R_{tđ}=R_4+R_{123}=4,4+1,5=5,9\Omega\)
\(I_m=\dfrac{\xi}{r+R_N}=\dfrac{12}{0,1+5,9}=2A\)
\(U_{AB}=2\cdot5,9=11,8V\)
b)\(I_4=I_{123}=I_m=2A\)
\(U_1=U_{23}=U_{123}=2\cdot1,5=3V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{3}{2}=1,5A\)
\(I_2=I_3=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{3}{6}=0,5A\)
\(U_{AC}=U_4+U_2=I_4\cdot R_4+I_2\cdot R_2=2\cdot4,4+0,5\cdot2=9,8V\)








