Cho hai điểm $A, B$ phân biệt. Xác định điểm $M$ biết $2 \overrightarrow{M A}-3 \overrightarrow{M B}=\overrightarrow{0}$
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 12 2022
a: vecto AB+2vecto BM=vecto 0
=>vecto AB=-2 vecto BM=-2 vecto MB
=>vecto BA=2 vecto BM
=>M là trung điểm của AB
b: =>2 vecto NA=3 vecto NB
=>vecto NA=3/2 vecto NB
=>NA=3/2NB và N nằm giữa A và B
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Cách 1:
\(\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} = - 4\overrightarrow {MB} \Rightarrow \frac{{MA}}{{MB}} = \frac{{\left| {\overrightarrow {MA} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = \frac{{\left| { - 4\overrightarrow {MB} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = 4\) và hai vectơ \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng
Suy ra M nằm giữa AB sao cho \(\frac{{MA}}{{MB}} = 4\)
Cách 2:
\(\begin{array}{l}
\overrightarrow {MA} + 4\overrightarrow {MB} = \vec 0\\
\Leftrightarrow \overrightarrow {MB} + \overrightarrow {BA} + 4\overrightarrow {MB} = \vec 0\\
\Leftrightarrow 5\overrightarrow {MB} = \overrightarrow {AB}
\end{array}\)
Vậy A, M, B thẳng hàng, M nằm giữa A và B sao cho \(MB = \frac{1}{5}AB\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) \(\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0 \)
\(\begin{array}{l}
\overrightarrow {OA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + \overrightarrow {BA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + 3\overrightarrow {OB} = - \overrightarrow {BA} \\
\Leftrightarrow 4\overrightarrow {OB} = \overrightarrow {AB} \\
\Leftrightarrow \overrightarrow {OB} = \frac{1}{4}\overrightarrow {AB}
\end{array}\)
Vậy O thuộc đoạn AB sao cho \(OB = \frac{1}{4}AB\)
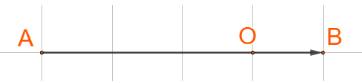
b) Ta có:
\(\begin{array}{l}
\overrightarrow {MA} + 3\overrightarrow {MB} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\\
= \left( {\overrightarrow {MO} + 3\overrightarrow {MO} } \right) + \left( {\overrightarrow {OA} + 3\overrightarrow {OB} } \right)\\
= 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} . (đpcm)
\end{array}\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a)
Cách 1:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\( \Leftrightarrow \overrightarrow {KA} = - 2\overrightarrow {KB} \)
Suy ra vecto \(\overrightarrow {KA} \) và vecto\(\;\overrightarrow {KB} \) cùng phương, ngược chiều và \(KA = 2.KB\)
\( \Rightarrow K,A,B\)thẳng hàng, K nằm giữa A và B thỏa mãn: \(KA = 2.KB\)
Cách 2:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\(\begin{array}{l} \Leftrightarrow \left( {\overrightarrow {KB} + \overrightarrow {BA} } \right) + 2\overrightarrow {KB} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} + \overrightarrow {BA} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} = \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {KB} = \frac{1}{3}\overrightarrow {AB} \end{array}\)
Vậy K thuộc đoạn AB sao cho \(KB = \frac{1}{3}AB\).
b)
Với O bất kì, ta có:
\(\frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} = \frac{1}{3}\left( {\overrightarrow {OK} + \overrightarrow {KA} } \right) + \frac{2}{3}\left( {\overrightarrow {OK} + \overrightarrow {KB} } \right) = \left( {\frac{1}{3}\overrightarrow {OK} + \frac{2}{3}\overrightarrow {OK} } \right) + \left( {\frac{1}{3}\overrightarrow {KA} + \frac{2}{3}\overrightarrow {KB} } \right) = \overrightarrow {OK} + \frac{1}{3}\left( {\overrightarrow {KA} + 2\overrightarrow {KB} } \right) = \overrightarrow {OK}\)
Vì \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \)
Vậy với mọi điểm O, ta có \(\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} .\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 10 2020
\(\Leftrightarrow2\overrightarrow{MA}+3\overrightarrow{BM}=\overrightarrow{0}\Leftrightarrow2\overrightarrow{MA}+3\left(\overrightarrow{BA}+\overrightarrow{AM}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}+3\overrightarrow{BA}=\overrightarrow{0}\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AB}\)
Vậy M là điểm nằm trên tia đối của tia BA sao cho \(AM=3AB\)
TK
gọi I là điểm thỏa mãn 2vt IA-3vt IB=vt 0
có 2 vecto MA - 3 vecto MB = vecto 0
<=>2vt MI+2vt IA -3vt MI-3vt IB=vt 0
<=>-vt MI=vt0
<=> vt IM= vt 0
<=> M trùng với I