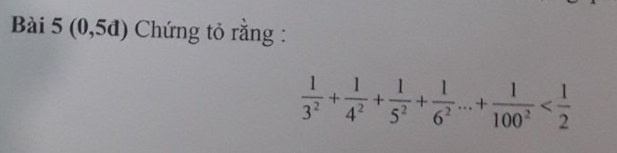
Mọi người giải chi tiết giúp em với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DK
1
21 tháng 10 2021
\(B=-x^2+2x-4\)
\(=-\left(x^2-2x+4\right)\)
\(=-\left(x-1\right)^2-3\le-3\forall x\)
Dấu '=' xảy ra khi x=-3
NM
0
NT
1
PT
3
11 tháng 3 2022
theo mình thì câu trên: dưới mẫu trong căn bỏ n^2 ra làm nhân tử chung xong đặt nhân tử chung của cả mẫu là n^2 . câu dưới thì mình k biết!!
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(\lim\dfrac{-3n+2}{n-\sqrt{4n+n^2}}=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{\left(n-\sqrt{4n+n^2}\right)\left(n+\sqrt{4n+n^2}\right)}\)
\(=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{-4n}=\lim\dfrac{n\left(-3+\dfrac{2}{n}\right)n\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4n}\)
\(=\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}\)
Do \(\lim\left(n\right)=+\infty\)
\(\lim\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=\dfrac{\left(-3+0\right)\left(1+\sqrt{0+1}\right)}{-4}=\dfrac{3}{2}>0\)
\(\Rightarrow\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=+\infty\)
QC
2
B
30 tháng 4 2022
pt 2CH3COOH+Mg→(CH3COO)2Mg +H2
n(CH3COO)2Mg =1,42/142=0,1 mol
theo pt nCH3COOH =2n(CH3COO)2Mg =0,2 mol
suy ra CM=0,2 /0,5=0.4 mol/l
theo pt nH2 =n(CH3COO)2Mg =0,1 mol
suy ra VH2 =2,24l
KOH+CH3COOH->CH3COOK+H2O
0,2------0,2
=>VKOH=\(\dfrac{0,2}{0,5}\)=0,4l=400ml
1 tháng 12 2021
Bài 2:
\(a,n_{H_2}=\dfrac{1,12}{22,4}=0,05(mol)\\ PTHH:Mg+2HCl\to MgCl_2+H_2\\ MgO+2HCl\to MgCl_2+H_2O\\ \Rightarrow n_{Mg}=0,05(mol)\\ \Rightarrow m_{Mg}=24.0,05=1,2(g)\\ \Rightarrow m_{MgO}=9,2-1,2=8(g) b,\%_{Mg}=\dfrac{1,2}{9,2}.100\%=13,04\%\\ \Rightarrow \%_{MgO}=100\%-13,04\%=86,96\%\\ c,n_{MgO}=\dfrac{8}{40}=0,2(mol)\\ \Rightarrow \Sigma n_{HCl}=2n_{Mg}+2n_{MgO}=0,5(mol)\\ \Rightarrow \Sigma m_{HCl}=0,5.36,5=18,25(g)\\ \Rightarrow m_{dd_{HCl}}=\dfrac{18,25}{14,6\%}=125(g)\)
\(\Leftrightarrow\dfrac{1}{3^2}+\dfrac{1}{4^2}+....+\dfrac{1}{100^2}< \dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\\ \Leftrightarrow Ta.thay:\\ \dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3};\dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4};...;\dfrac{1}{99.100}=\dfrac{1}{99}-\dfrac{1}{100}\\ \Leftrightarrow A< \dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ \Leftrightarrow A< \dfrac{1}{2}-\dfrac{1}{100}< \dfrac{1}{2}\\ \Rightarrow A< \dfrac{1}{2}\\ \Rightarrow\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\left(đpcm\right)\)