Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm A và B gọi M là điểm tùy ý trên đường thẳng AB nằm ngoài đoạn AB . Qua M vẽ hai cát tuyến MCD và MC'D' của đường tròn (O) và (O'). Chứng minh tứ giác CDC'D' nội tiếp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 5 2017
(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’ 
ΔPBO
⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên:
O ’ P 2 = O ’ A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π . r 2 = 2 π ( c m 2 ) .
CM
28 tháng 2 2017
(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’ 
ΔPBO
⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên: O ' P 2 = O ' A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π · r 2 = 2 π cm 2
25 tháng 4 2017
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (o),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').
Hướng dẫn làm bài:
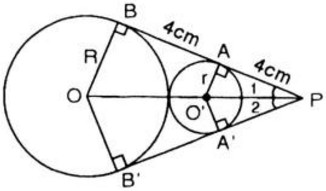
Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
ˆA=ˆB=900A^=B^=900
ˆP1P1^ chung
Vậy ΔOBP ~ ∆ O’AP
⇒rR=PO′PO=PAPB=48=12⇒R=2r⇒rR=PO′PO=PAPB=48=12⇒R=2r
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)
KD
25 tháng 4 2017
Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
chung
Vậy ΔOBP ~ ∆ O’AP
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)
9 tháng 5 2023
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD=AH*AO
10 tháng 4 2023
a: góc BMA=góc CNA=90 độ
=>MB//NC
=>IK//MB//NC
=>IK vuông góc MN
góc AIK+góc AHK=90+90=180 độ
=>AHIK nội tiếp
b: ΔHMN đồng dạng với ΔABC
=>góc MHN=góc BAC cố định
\(S_{HMN}=\dfrac{1}{2}\cdot HM\cdot HN\cdot sin\widehat{MHN}< =\dfrac{1}{2}\cdot AB\cdot AC\cdot sin\widehat{BAC}\)
Dấu = xảy ra khi MH là đừog kính của (O) và NH là đường kính của (O')
CM
22 tháng 1 2019
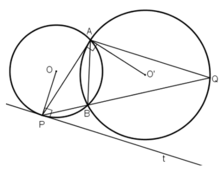
Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
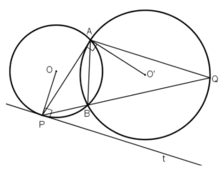
Xét ΔMC'A và ΔMBD' có
góc MC'A=góc MBD'
góc M chung
=>ΔMC'A đồng dạng với ΔMBD'
=>MC'/MB=MA/MD'
=>MC'*MD'=MA*MB
Xét ΔMAC và ΔMDB có
góc MAC=góc MDB
góc M chung
=>ΔMAC đồng dạng với ΔMDB
=>MA/MD=MC/MB
=>MA*MB=MD*MC
=>MD*MC=MC'*MD'
=>MD/MC'=MD'/MC
=>ΔMDD' đồng dạng với ΔMC'C
=>góc MDD'=góc MC'C
=>góc D'C'C+góc D'DC=180 độ
=>CDC'D' nội tiếp