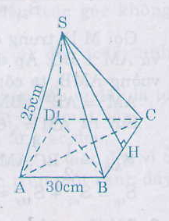
một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm đáy là hình vuông ABCD có cạnh là 30cm tính diện tích toàn phần cảu hình chóp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

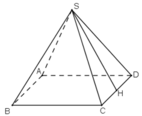
Gọi H là trung điểm của CD
Vì ΔSCD cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
⇒ SH ⊥ CD.
Ta có:
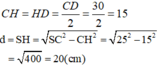
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp:
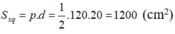
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)

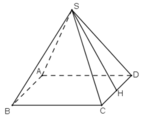
Gọi H là trung điểm của CD
Vì ΔSCD cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
⇒ SH ⊥ CD.
Ta có:
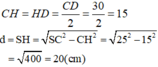
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp:
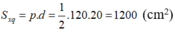
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)

Gọi M là trung điểm của BC thì SM là đường cao của mặt bên SBC (vì tam giác SBC cân tại S)
Áp dụng công thức: Stp = Sxq + Sd
Ta có: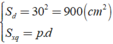 (với p = 60( cm ) )
(với p = 60( cm ) )
Áp dụng định lí Py – ta – go vào tam giác SCM vuông tại M
SC2 = CM2 + SM2 ⇒ 252 = 152 + SM2 ⇔ SM2 = 202 ⇔ SM = 20( cm )
Do đó: Sxq = 60.20 = 1200( cm2 ) ⇒ Stp = 1200 + 900 = 2100( cm2 )

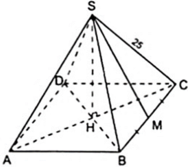
Gọi M là trung điểm của BC thì SM là đường cao của mặt bên SBC (vì tam giác SBC cân tại S)
Áp dụng công thức:


gọi SI là trung đoạn của hình chóp tứ giác đều S.ABCD và I là trung điểm của đoạn CD
=> SI là đường trung tuyến đồng thời cũng là đường cao trong tam giác cân SCD
xét tam giác SID vuông tại I có:
SD^2= ID^2+SI^2
=> SI= 20cm
ta có Sxq = p.d= [( 25+25+30):2].20=800cm2
Stp=Sxq+ Sđ= 800+(30.30)=1700cm2
Gọi H là trung điểm của CD
Vì \(\Delta SCD\) cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
.\(\Rightarrow SH\perp CD\)
Ta có :
\(CH=HD=\frac{CD}{2}=\frac{30}{2}=15\)
\(d=SH=\sqrt{SC^2-CH^2}=\sqrt{25^2-15^2}\)
\(=\sqrt{400}=20\left(cm\right)\)
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp :
\(S_{xq}=p.d=\frac{1}{2}.120.20=1200\left(cm^2\right)\)
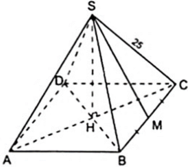
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)

Ta có : \(d=SH=\sqrt{SB^2-BH^2}\)
\(=\sqrt{25^2-15^2}=\sqrt{400}=20\left(cm\right)\)
Diện tích xung quanh của hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).30.4.20 = 1200 (cm2)
Diện tích đáy: Sđ = 302 = 900(cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 1200 + 900 = 2100(cm2)
S.ABCD là hình chóp tứ giác đều
=>SO vuông góc (ABCD), O là giao của AC và BD
AC=BD=căn 30^2+30^2=30*căn 2(cm)
=>AO=BO=15*căn 2(cm)
SO=căn SA^2-AO^2=căn 25^2-450=5*căn 7(cm)
Sxq=5*căn 7*30*2=300*căn 7(cm2)
Stp=300*căn 7+30^2=300*căn 7+900(cm2)