Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
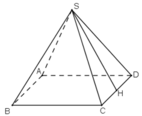
Gọi H là trung điểm của CD
Vì ΔSCD cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
⇒ SH ⊥ CD.
Ta có:
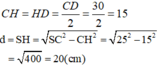
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp:
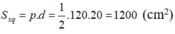
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)
S.ABCD là hình chóp tứ giác đều
=>SO vuông góc (ABCD), O là giao của AC và BD
AC=BD=căn 30^2+30^2=30*căn 2(cm)
=>AO=BO=15*căn 2(cm)
SO=căn SA^2-AO^2=căn 25^2-450=5*căn 7(cm)
Sxq=5*căn 7*30*2=300*căn 7(cm2)
Stp=300*căn 7+30^2=300*căn 7+900(cm2)
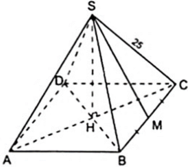
Gọi M là trung điểm của BC thì SM là đường cao của mặt bên SBC (vì tam giác SBC cân tại S)
Áp dụng công thức: Stp = Sxq + Sd
Ta có: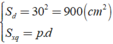
(với p = 60( cm ) )
Áp dụng định lí Py – ta – go vào tam giác SCM vuông tại M
SC2 = CM2 + SM2 ⇒ 252 = 152 + SM2 ⇔ SM2 = 202 ⇔ SM = 20( cm )
Do đó: Sxq = 60.20 = 1200( cm2 ) ⇒ Stp = 1200 + 900 = 2100( cm2 )
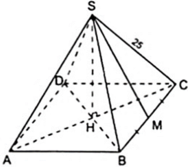
Gọi M là trung điểm của BC thì SM là đường cao của mặt bên SBC (vì tam giác SBC cân tại S)
Áp dụng công thức:
gọi SI là trung đoạn của hình chóp tứ giác đều S.ABCD và I là trung điểm của đoạn CD
=> SI là đường trung tuyến đồng thời cũng là đường cao trong tam giác cân SCD
xét tam giác SID vuông tại I có:
SD^2= ID^2+SI^2
=> SI= 20cm
ta có Sxq = p.d= [( 25+25+30):2].20=800cm2
Stp=Sxq+ Sđ= 800+(30.30)=1700cm2
Gọi H là trung điểm của CD
Vì \(\Delta SCD\) cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
.\(\Rightarrow SH\perp CD\)
Ta có :
\(CH=HD=\frac{CD}{2}=\frac{30}{2}=15\)
\(d=SH=\sqrt{SC^2-CH^2}=\sqrt{25^2-15^2}\)
\(=\sqrt{400}=20\left(cm\right)\)
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp :
\(S_{xq}=p.d=\frac{1}{2}.120.20=1200\left(cm^2\right)\)
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)
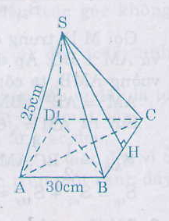
Ta có : \(d=SH=\sqrt{SB^2-BH^2}\)
\(=\sqrt{25^2-15^2}=\sqrt{400}=20\left(cm\right)\)
Diện tích xung quanh của hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).30.4.20 = 1200 (cm2)
Diện tích đáy: Sđ = 302 = 900(cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 1200 + 900 = 2100(cm2)
Gọi H là trung điểm của CD
Vì ΔSCD cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
⇒ SH ⊥ CD.
Ta có:
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp:
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)