a) 3x – 12 = 0
b) ( x – 2 )( 3x + 3 ) = 0
c) 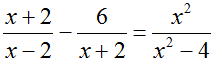
các bn giúp mik với !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a \(\Leftrightarrow3x=12\Leftrightarrow x=4\)
b \(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{3}{2}\end{matrix}\right.\)
c \(ĐKXĐ:x\ne2;x\ne-2\)
\(\Rightarrow\left(x+2\right)^2-6\left(x-2\right)=x^2\Leftrightarrow x^2+4x+4-6x+12=x^2\Leftrightarrow-2x+16=0\Leftrightarrow-2x=-16\Leftrightarrow x=8\left(TM\right)\)
a) Ta có: 3x-12=0
\(\Leftrightarrow3x=12\)
hay x=4
Vậy: S={4}
b) Ta có: (x-2)(2x+3)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-3}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{2;\dfrac{-3}{2}\right\}\)

Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:
a) 2 + x = 0
b) 3x2 – 3x + 1 = 0
c) 1 – 12u = 0
d) -3 = 0
e) 4y = 12

\(a,=3x-9-4x+12=-x+3=0\)
\(\Leftrightarrow x=3\)
Vậy ..
\(b,=\left(x+2\right)\left(x+2-x+2\right)=4\left(x+2\right)=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)
Vậy ..
\(c,=x^3-3x^2+3x-1=\left(x-1\right)^3=0\)
\(\Leftrightarrow x=1\)
Vậy ..
\(d,\Leftrightarrow x\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
Vậy ..
\(e,=\left(2x-3-5\right)\left(2x-3+5\right)=\left(2x-8\right)\left(2x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{2}=4\\x=-\dfrac{2}{2}=-1\end{matrix}\right.\)
Vậy ...
a) Ta có: 3(x-3)-4x+12=0
\(\Leftrightarrow3\left(x-3\right)-4\left(x-3\right)=0\)
\(\Leftrightarrow x-3=0\)
hay x=3
Vậy: S={3}
b) Ta có: \(\left(x+2\right)^2-\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow x^2+4x+4-x^2+4=0\)
\(\Leftrightarrow4x=-8\)
hay x=-2
Vậy: S={-2}
c) Ta có: \(x^3+3x=3x^2+1\)
\(\Leftrightarrow x^3-3x^2+3x-1=0\)
\(\Leftrightarrow x-1=0\)
hay x=1
Vậy: S={1}
d) Ta có: \(\dfrac{2}{3}x\left(x^2-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
Vậy: S={0;2;-2}

a) 4x – 20 = 0
⇔ 4x = 20
⇔ x = 20 : 4
⇔ x = 5
Vậy phương trình có nghiệm duy nhất x = 5.
b) 2x + x + 12 = 0
⇔ 3x + 12 = 0
⇔ 3x = -12
⇔ x = -12 : 3
⇔ x = -4
Vậy phương trình đã cho có nghiệm duy nhất x = -4
c) x – 5 = 3 – x
⇔ x + x = 5 + 3
⇔ 2x = 8
⇔ x = 8 : 2
⇔ x = 4
Vậy phương trình có nghiệm duy nhất x = 4
d) 7 – 3x = 9 – x
⇔ 7 – 9 = 3x – x
⇔ -2 = 2x
⇔ -2 : 2 = x
⇔ -1 = x
⇔ x = -1
Vậy phương trình có nghiệm duy nhất x = -1.
Em lớp 6 em chỉ làm dc phần a,b,c
Kết quả như sau:
a,4x-20=0
4x=20+0
4x=20
x=20:4
x=5

a: \(\Leftrightarrow3x\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{5}\end{matrix}\right.\)

a: =>(x-5)(x+5)+(x-5)(3x-15)=0
=>(x-5)(x+5+3x-15)=0
=>(x-5)(4x-10)=0
=>x=5 hoặc x=5/2
c: =>x^3-3x^2+2x^2-6x-8x+24=0
=>(x-3)(x^2+2x-8)=0
=>(x-3)(x+4)(x-2)=0
=>\(x\in\left\{3;-4;2\right\}\)

(x-1)(2x^2-8)=0
\(\Leftrightarrow\left(x-1\right)\left(2x^2-8\right)=0\\ \left(2x^3-8x-2x^2+8\right)=0\)
\(\Leftrightarrow2x\left(x-1\right)-8\left(x-1\right)=0\)
\(\Leftrightarrow x=1;x=\dfrac{8}{2}\)
3x^2-8x+5=0
áp dụng công thức bậc 2 ta có:
\(x=\dfrac{-\left(-8\right)\pm\sqrt{\left(-8\right)^2-4.3.5}}{2.3}\)
\(\Rightarrow x=\dfrac{5}{3};x=1\)
(7x-1).2x-7x+1=0
\(\Leftrightarrow\left(7x-1\right)\left(2x-1\right)=0\)
\(\Leftrightarrow x=\dfrac{1}{7};x=\dfrac{1}{2}\)

3:
a: u+v=14 và uv=40
=>u,v là nghiệm của pt là x^2-14x+40=0
=>x=4 hoặc x=10
=>(u,v)=(4;10) hoặc (u,v)=(10;4)
b: u+v=-7 và uv=12
=>u,v là các nghiệm của pt:
x^2+7x+12=0
=>x=-3 hoặc x=-4
=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)
c; u+v=-5 và uv=-24
=>u,v là các nghiệm của phương trình:
x^2+5x-24=0
=>x=-8 hoặc x=3
=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)
\(a,3x-12=0\)
\(\Leftrightarrow3x=12\)
\(\Leftrightarrow x=4\)
Vậy \(S=\left\{4\right\}\)
\(b,\left(x-2\right)\left(3x+3\right)=0\)
\(\cdot TH1:x-2=0\)
\(\Leftrightarrow x=2\)
\(\cdot TH2:3x+3=0\)
\(\Leftrightarrow x=-1\)
vậy \(S=\left\{-1;2\right\}\)
\(c,\dfrac{x+2}{x-2}-\dfrac{6}{x+2}=\dfrac{x^2}{x^2-4}\left(ĐKXĐ:x\ne2;x\ne-2\right)\)
\(\Leftrightarrow\left(x+2\right)\left(x+2\right)-6\left(x-2\right)=x^2\)
\(\Leftrightarrow x^2+2x+2x+4-6x+12=x^2\)
\(\Leftrightarrow x^2-x^2+2x+2x-6x+4+12=0\)
\(\Leftrightarrow-2x+16=0\)
\(\Leftrightarrow-2x=-16\)
\(\Leftrightarrow x=8\left(nhận\right)\)
Vậy S\(S=\left\{8\right\}\)
a) 3x-12=0
⟺3x=12⟺x=4
Vậy tập nghiệm của phương trình là S={4}
b) (x-2)(3x+3)=0
⟺ x-2=0 ⟺x=2 ⟺x=2
3x+3=0 ⟺3x=-3 ⟺x=-1
Vậy tập nghiệm của phương trình là S={2;-1}
c)
x-2≠0 x-2≠0 x≠2
ĐKXĐ x+2≠0 ⟺ x+2≠0 ⟺ x ≠-2
x2-4=(x-2)(x+2)≠0
x+2/x-2 - 6/x+2 = x2/x2-4
⟺ (x+2)(x+2)/(x-2)(x+2) - 6(x-2)/(x-2)(x+2) = x2/(x-2)(x+2)
⟺(x+2)(x+2) - 6(x-2)=x2
⟺(x+2)(x+2-6)=x2
⟺(x+2)(x-4)-x2=0
⟺x2-4x+2x-8-x2=0
⟺-2x-8=0
⟺-2x=8
⟺x=-4
Vập tập nghiệm của phương trình là S={-4}