tìm các số a,b,c, biết a phần 2 =b phần 3 và a2-b2+2c2=108 (tính chất dãy tỉ số bằng nhau)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
20 tháng 1 2018
Ta có:
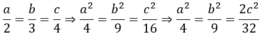
Theo tính chất dãy tỉ số bằng nhau ta có:
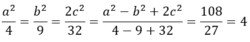
Ta có:
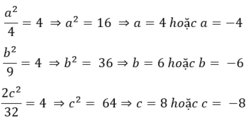
Mà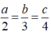 
nên a, b và c cùng dấu.
Vậy ta tìm được các số a1 = 4; b1 = 6; c1 = 8 hoặc a2 = -4; b2 = -6 và c2 = -8
S
29 tháng 12 2020
a) \(\dfrac{a}{5}=\dfrac{b}{4}\Rightarrow\dfrac{a^2}{25}=\dfrac{b^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{25}=\dfrac{b^2}{16}=\dfrac{a^2-b^2}{25-16}=\dfrac{1}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{1}{9}\cdot25=\dfrac{25}{9}\\b^2=\dfrac{1}{9}\cdot16=\dfrac{16}{9}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3};b=\dfrac{4}{3}\\a=\dfrac{-5}{3};b=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(\left(a;b\right)\in\left\{\left(\dfrac{5}{3};\dfrac{4}{3}\right);\left(-\dfrac{5}{3};-\dfrac{4}{3}\right)\right\}\)
b) \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=4.4=16\\b^2=4.9=36\\c^2=4,16=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=4;=6;c=8\\a=-4;b=-6;c=-8\end{matrix}\right.\)
Vậy (a;b;c) \(\in\left\{\left(4;6;8\right);\left(-4;-6;-8\right)\right\}\)
T
2
2 tháng 11 2021
Sửa \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\Rightarrow a=2k;b=3k;c=4k\)
\(a^2-b^2+2c^2=108\\ \Rightarrow4k^2-9k^2+32k^2=108\\ \Rightarrow27k^2=108\Rightarrow k^2=4\\ \Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4;y=6;z=8\\x=-4;y=-6;z=-8\end{matrix}\right.\)
TH
2 tháng 11 2021
Ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a^2}{2^2}=\dfrac{b^2}{3^2}=\dfrac{2c^2}{2.4^2}=\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}\)
Áp dụng tcdtsbn , ta có:
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a=8\\b=12\\c=16\end{matrix}\right.\)
29 tháng 7 2021
Bài 1:
Uses crt;
var i,n,j:integer;
a,b,c:array[1..100000] of integer;
Begin
clrscr;
readln(n);
for i:= 1 to n do readln(a[i]);
for i:= 1 to n do readln(b[i]);
j:=0;
for i:= 1 to n do
Begin
inc(j);
c[j] := a[i];
inc(j);
c[j] := b[i];
end;
for i:= 1 to j do write(c[i],' ');
readln;
end.
22 tháng 5 2022
P≤√a2+2√aab+2b2+√b2+2√2bc+2c2+√c2+2√2ca+2a2P≤a2+2aab+2b2+b2+22bc+2c2+c2+22ca+2a2
P≤√(a+√2b)2+√(b+√2c)2+√(c+√2a)2P≤(a+2b)2+(b+2c)2+(c+2a)2
P≤(1+√2)(a+b+c)=1+√2P≤(1+2)(a+b+c)=1+2
Dấu "=" xảy ra khi (a;b;c)=(0;0;1)(a;b;c)=(0;0;1) và các hoán vị
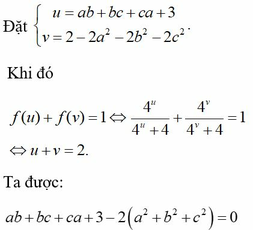
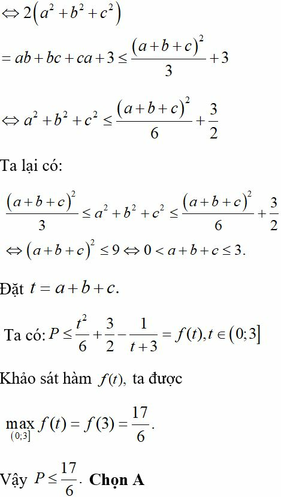
Theo tính chất dãy tỉ số bằng nhau
Ta có : a phần 2 =b phần 3 =a2-b2+2c2 phần 4-9+4=108 phần 9 =12
suy ra a=12x2=24
suy ra b=12x3=36
suy ra c =12x4=48
Vậy a=24
b=36
c=48