giúp mình phần I nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
2
15 tháng 10 2023
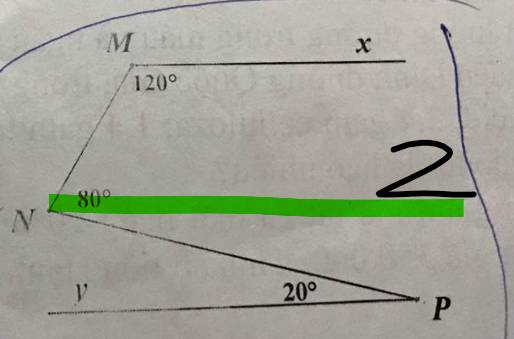
Qua N, kẻ tia Nz//Mx
Nz//Mx
=>\(\widehat{zNM}+\widehat{M}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{zNM}=60^0\)
\(\widehat{zNM}+\widehat{zNP}=\widehat{MNP}\)
=>\(\widehat{zNP}=80^0-60^0=20^0\)
\(\widehat{zNP}=\widehat{P}\)
mà hai góc này ở vị trí so le trong
nên Nz//Py
=>Mx//Py
NT
1
NT
2
H9
HT.Phong (9A5)
CTVHS
10 tháng 8 2023
\(\dfrac{1}{3}+\dfrac{2}{5}+\dfrac{2}{3}+\dfrac{2}{3}\)
\(=\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\left(\dfrac{2}{5}+\dfrac{2}{3}\right)\)
\(=\dfrac{3}{3}+\dfrac{16}{15}\)
\(=1+\dfrac{16}{15}\)
\(=\dfrac{15}{15}+\dfrac{16}{15}\)
\(=\dfrac{31}{15}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 8 2023
\(\dfrac{1}{3}+\dfrac{2}{5}+\dfrac{2}{3}+\dfrac{2}{3}=\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\dfrac{2}{5}+\dfrac{2}{3}=1+\dfrac{2}{5}+\dfrac{2}{3}=\dfrac{5}{3}+\dfrac{2}{5}=\dfrac{5\times5+2\times3}{15}=\dfrac{31}{15}\)
11 tháng 8 2021
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AC^2=CH\cdot CB\)