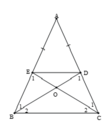
Cho tam giác ABC. Gọi D, E là các điểm thuộc cạnh AC và BC sao cho DA=DC và EC=2EB. CMR AE đi qua trung điểm của BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mik cho gợi ý thôi né :cậu c/m cho :
S2=S5 => S1=S4
Mà S tam giác ABM=S tam giác AMC=/2S tam giác ABC
C/m :S1+S2+S3 =S4+S5+S6=1/2 S tam giác ABC
=> Đpcm
Chúc bạn học tốt nha!

B,E,I thẳng hàng nên ta có:
\(\dfrac{IA}{IC}\cdot\dfrac{ED}{EA}\cdot\dfrac{BC}{BD}=1\)
=>\(\dfrac{IA}{IC}\cdot\dfrac{1}{2}\cdot\dfrac{5}{2}=1\)
=>\(\dfrac{IA}{IC}\cdot\dfrac{5}{4}=1\)
=>\(\dfrac{IA}{IC}=\dfrac{4}{5}\)

từ I kẻ IM vuông góc AC , từ B kẻ BN vuông góc AC => IM // BN
áp dụng định lý Menelous vào tam giác BCD có 3 điểm A ,I , E thẳng hàng và cắt 3 cạnh tam giác :
\(\dfrac{EC}{EB}\cdot\dfrac{IB}{ID}\cdot\dfrac{AD}{AC}=1\)
=> 2 . \(\dfrac{IB}{ID}\) . 3/4 = 1
=> \(\dfrac{IB}{ID}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{DI}{DB}=\dfrac{3}{7}\)
Do IM // BN => \(\dfrac{DI}{DB}=\dfrac{IM}{BN}=\dfrac{3}{7}\)
S abc = \(\dfrac{1}{2}BN\cdot AC\)
S iad = \(\dfrac{1}{2}IM\cdot AD\) \(\Rightarrow\dfrac{Siad}{Sabc}=\dfrac{IM}{BN}\cdot\dfrac{AD}{AC}=\dfrac{3}{7}\cdot\dfrac{3}{4}=\dfrac{9}{28}\)
mà S iad = 18 => S abc = 28*18 : 9 = 56