Giúp mình nhé 🥲🥲🥲🥲 mik ko bt T.A thật hic
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
Chỗ này là để hỏi bài hay hoặc khó chứ ko phải là chỗ để tìm người nếu muốn thì cứ lên đồn công an mà hỏi nhé bạn

14: \(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}=\dfrac{4}{4x+7}\)

\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)
\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\)
Suy ra : a/b = 2/3 => a - b = -1

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=9+144=153\)
=>\(BC=3\sqrt{17}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}=4\)
=>\(\widehat{B}\simeq75^057'\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN\(\sim\)ΔACB

\(72.\)
Xét tam giác AHC vuông tại H ta có:
\(\sin C=\dfrac{AH}{AC}\) (Tỉ số lượng giác).
\(\Rightarrow\sin30^o=\dfrac{AH}{40}.\Rightarrow AH=20.\)
Xét tam giác AHB vuông tại H:
\(AB^2=AH^2+BH^2\left(Pytago\right).\)
\(\Rightarrow29^2=20^2+BH^2.\\ \Leftrightarrow BH^2=29^2-20^2.\\ \Rightarrow BH=21.\)


=>2/6+2/12+2/20+...+2/x(x+1)=1010/1011
=>2(1/6+1/12+...+1/x(x+1))=1010/1011
=>1/2-1/3+1/3-1/4+...+1/x-1/x+1=505/1011
=>1/x+1=1/2022
=>x+1=2022
=>x=2021



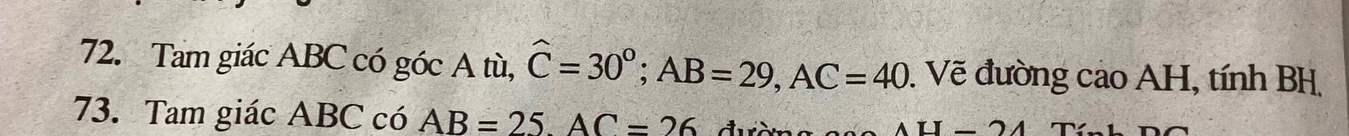 bài 72 giúp em 🥲🥲
bài 72 giúp em 🥲🥲


