Bài 7: Tính giá trị của biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A=0x^2y^4z+\dfrac{7}{2}x^2y^4z-\dfrac{2}{5}x^2y^4z=\dfrac{31}{10}x^2y^4z=\dfrac{31}{10}\cdot2^2\cdot\dfrac{1}{16}\cdot\left(-1\right)=-\dfrac{31}{40}\)
a: \(=\dfrac{7}{5}x^4z^3y=\dfrac{7}{5}\cdot2^4\cdot\left(-1\right)^3\cdot\dfrac{1}{2}=-\dfrac{56}{5}\)
b: \(=-xy^3\)

a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=8x^3-1-7x^3-7=x^3-8\)
b: Thay x=-1/2 vào A, ta được:
\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)

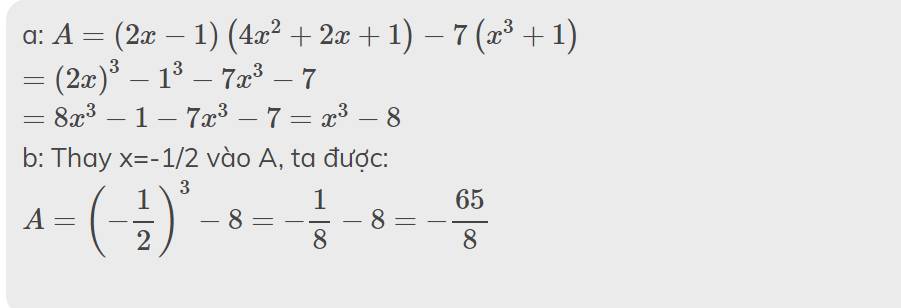
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
Để A là số nguyên tố thì x-2=1
=>x=3

a. 2205 - (35 . 7)
= 2205 - 245
= 1960
b. 8700 : 25 . 4
= 348 . 4
= 1392

Bài 1: A = (\(\dfrac{7}{13}\) + \(\dfrac{6}{13}\)) x 100 - 13 x a
Thay a = 10 vào A ta có:
A = (\(\dfrac{7}{13}\) + \(\dfrac{6}{13}\)) x 100 - 13 x 10
A = \(\dfrac{13}{13}\) x 100 - 130
A = 100 - 130
A = - 30
Thay a = 987 vào biểu thức A ta có:
A = (\(\dfrac{7}{13}\) + \(\dfrac{6}{13}\)) x 100 - 13 x 987
A = \(\dfrac{13}{13}\) x 100 - 12831
A = 100 - 12831
A = -12731


Bài 1 :
\(N=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
Ta có : \(x+y+z=0\Rightarrow x+y=-z;y+z=-x;x+z=-y\)
hay \(-z.\left(-x\right)\left(-y\right)=-zxy\)
mà \(xyz=2\Rightarrow-xyz=-2\)
hay N nhận giá trị -2
Bài 2 :
\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)Đặt \(a=10k;b=3k\)
hay \(\frac{30k-6k}{10k-9k}=\frac{24k}{k}=24\)
hay biểu thức trên nhận giá trị là 24
c, Ta có : \(a-b=3\Rightarrow a=3+b\)
hay \(\frac{3+b-8}{b-5}-\frac{4\left(3+b\right)-b}{3\left(3+b\right)+3}=\frac{-5+b}{b-5}-\frac{12+4b-b}{9+3b+3}\)
\(=\frac{-5+b}{b-5}-\frac{12+3b}{6+3b}\)quy đồng lên rút gọn, đơn giản rồi
1.Ta có:\(x+y+z=0\)
\(\Rightarrow\hept{\begin{cases}x+y=-z\\y+z=-x\\x+z=-y\end{cases}}\)
\(\Rightarrow N=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\left(-x\right)\left(-y\right)=-2\)
2.Ta có:\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)
Đặt \(\frac{a}{10}=\frac{b}{3}=k\Rightarrow a=10k;b=3k\)
Ta có:\(A=\frac{3a-2b}{a-3b}=\frac{3.10k-2.3k}{10k-3.3k}=\frac{30k-6k}{10k-9k}=\frac{k\left(30-6\right)}{k\left(10-9\right)}=24\)
Vậy....
241/210
A = \(\dfrac{3}{2}-\dfrac{5}{6}+\dfrac{7}{12}-\dfrac{9}{20}+\dfrac{11}{30}-\dfrac{13}{42}+\dfrac{15}{56}-\dfrac{17}{72}+\dfrac{19}{90}\)
A \(=\dfrac{3}{1\cdot2}-\dfrac{5}{2\cdot3}+\dfrac{7}{3\cdot4}-\dfrac{9}{4\cdot5}+\dfrac{11}{5\cdot6}-\dfrac{13}{6\cdot7}+\dfrac{15}{7\cdot8}-\dfrac{17}{8\cdot9}+\dfrac{19}{9\cdot10}\)
A
\(=\left(1+\dfrac{1}{2}\right)+\left(\dfrac{1}{2}+\dfrac{2}{3}\right)+\left(\dfrac{1}{3}+\dfrac{3}{4}\right)+\left(\dfrac{1}{4}+\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)+\left(\dfrac{1}{6}+\dfrac{1}{7}\right)+\left(\dfrac{1}{7}+\dfrac{7}{8}\right)+\left(\dfrac{1}{8}+\dfrac{1}{9}\right)+\left(\dfrac{1}{9}+\dfrac{1}{10}\right)\)
\(A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\)
A = \(1-\dfrac{1}{10}=\dfrac{9}{10}\)