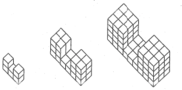
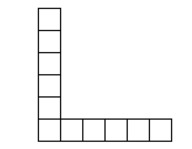
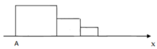
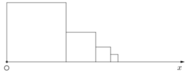
Bạn Thùy xếp các hình vuông thành các hình theo quy luật như dưới đây. Hỏi nếu cứ tiếp
tục như vậy thì hình thứ bao nhiêu sẽ được xếp bởi 6044 hình vuông nhỏ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mỗi một chu kì là: hình tam giác, hình vuông, hình tròn, hình chữ nhật. Gồm \(4\)hình.
Thực hiện phép chia có dư: \(203=50\times4+3\)do đó đến hình thứ \(203\)sẽ có \(50\)chu kì và thêm \(3\)hình đầu tiên đó là hình tam giác, hình vuông, hình tròn.
Nhu vậy, số hình vuông xuất hiện là \(50+1=51\).

Khi vẽ hình thứ 3,ta có:
Số hình lập phương đơn vị bên trái là 3.4.3=36
Số hình lập phương đơn vị bên trái là 3.4.3 =36
Số hình lập phương đơn vị ở giữa là 3.3=9
Vậy có tổng số :36+36+9=81 hình lập phương đơn vị
Với quy luật đó thì hình thứ 10:
Số hình lập phương đơn vị bên trái là 10.11.10=1100
Số hình lập phương đơn vị bên trái là 10.11.10=1100
Số hình lập phương đơn vị ở giữa là 10.10 =100
Vậy tổng số hình lập phương đơn vị của hình thứ 10 là:
1100 + 1100 +100=2300 (hình)

số thứ 5 là : 819 : 9 = 91
số thứ 4 là : 91 - 1 = 90
số thứ 3 là : 90 - 1 = 89
số thứ 2 là : 89 - 1 = 88
số thứ 1 là : 88 - 1 = 87
số thứ 6 là : 91 + 1 = 92
số thứ 7 là : 92 + 1 = 93
số thứ 8 là : 92 + 1 = 93
số thứ 9 là : 93 + 1 = 94

Đáp án B.
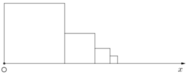
Tổng các cạnh nằm trên tia Ox của các canh hình vuông đó là:
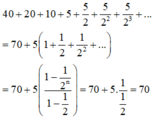

Chọn B
Tổng các cạnh nằm trên tia Ax của các hình vuông đó là
10 + 5 + 5 2 + 5 2 2 + . . . = 20 ( c m )

Đáp án B.
Tổng các cạnh nằm trên tia Ox của các canh hình vuông đó là: