Phân tích đa thức thành nhân tử
x2(y-z)+y2(z-x)+z2(x-y)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 10 2017
x 2 y + x y 2 + x 2 z + x z 2 + y 2 z + y z 2 + 3xyz.
= ( x 2 y + x 2 z + xyz) + (x y 2 + y 2 z + xyz) + (x z 2 + y z 2 + xyz)
= x(xy + xz + yz) + y(xy + yz + xz) + z(xz + yz + xy)
= (x + y + z)(xy + xz + yz).
NC
14 tháng 12 2020
\(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+3xyz\)
\(=\left(x^2y+x^2z+xyz\right)+\left(xz^2+yz^2+xyz\right)+\left(xy^2+y^2z+xyz\right)\)
\(=x\left(xy+xz+yz\right)+z\left(xz+yz+xy\right)+y\left(xy+yz+xz\right)\)
\(=\left(x+y+z\right)\left(xy+yz+xz\right)\)
PT
1
H
12 tháng 10 2023
`x^2 -4x+4-y^2`
`=(x^2 -4x+4)-y^2`
`=(x-2)^2 -y^2`
`=(x-2-y)(x-2+y)`
`x^2+2xy+y^2-x-y`
`=(x^2+2xy+y^2) -(x+y)`
`=(x+y)^2 -(x+y)`
`=(x+y)(x+y-1)`
`x^2-2xy+y^2-9`
`=(x^2-2xy+y^2)-3^2`
`=(x-y)^2-3^3`
`=(x-y-3)(x-y+3)`
Tách ra đi cậu.
23 tháng 8 2021
\(A=x\left(y^2-z^2\right)+y\left(z^2-x^2\right)+z\left(x^2-y^2\right)=x\left(y^2-z^2\right)+y\left(-y^2+z^2-x^2+y^2\right)+z\left(x^2-y^2\right)=\left(y^2-z^2\right)\left(x-y\right)+\left(x^2-y^2\right)\left(z-y\right)=\left(y-z\right)\left(y+z\right)\left(x-y\right)-\left(x-y\right)\left(x+y\right)\left(y-z\right)=\left(x-y\right)\left(y-z\right)\left(y+z-x-y\right)=\left(x-y\right)\left(y-z\right)\left(z-x\right)\)
23 tháng 8 2021
\(B=a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)=ab^3-ac^3+bc^3-a^3b+a^3c-b^3c=ab\left(b^2-a^2\right)-c^3\left(a-b\right)+c\left(a^3-b^3\right)=-ab\left(a-b\right)\left(a+b\right)-c^3\left(a-b\right)+c\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)\left(-a^2b-ab^2-c^3+a^2c+abc+b^2c\right)\)
TL
1
18 tháng 10 2021
Do câu d mình ko biết làm bởi v mình không làm được
VT
2
11 tháng 10 2021
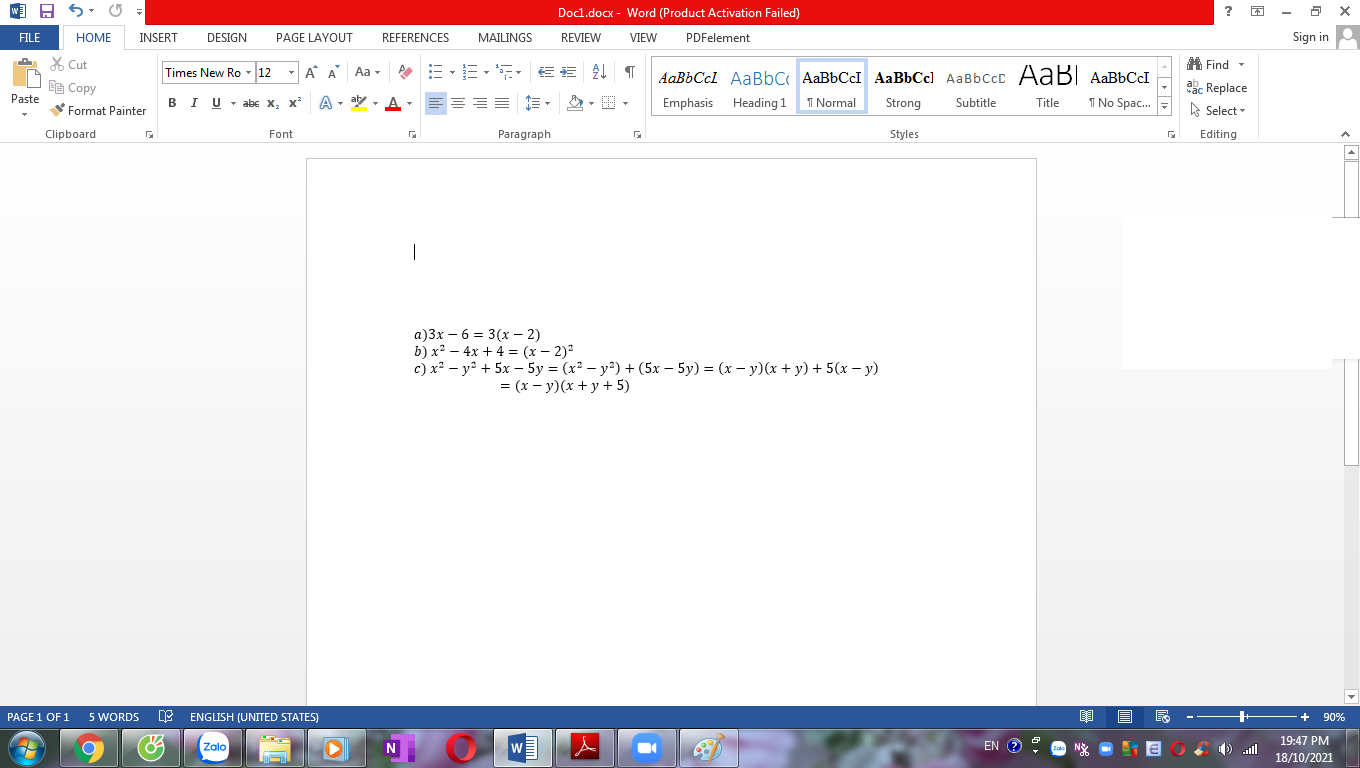
\(x^2-4y^2-2x+1=\left(x-1\right)^2-4y^2=\left(x-1-2y\right)\left(x-1+2y\right)\)
NT
0
\(=x^2y-x^2z+y^2z-y^2x+z^2\left(x-y\right)\)
\(=x^2y-y^2x-x^2z+y^2z+z^2\left(x-y\right)\)
\(=xy\left(x-y\right)-z\left(x^2-y^2\right)+z^2\left(x-y\right)\)
\(=\left(x-y\right)\left(xy-z\left(x+y\right)+z^2\right)\)
\(=\left(x-y\right)\left(xy-zx+z^2-zy\right)=\left(x-y\right)\left[x\left(y-z\right)-z\left(y-z\right)\right]\)
\(=\left(x-y\right)\left(y-z\right)\left(x-z\right)\)