Cho \(\Delta\)\(ABC\) vuông tại A, có chu vi =60cm, và cạnh huyền BC=25cm. Tính các cạnh góc vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
0
QD
23 tháng 5 2016
Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25
độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)
Theo đề bài ta có pt :
x + (35 - x ) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0
Δ = (−35)2 − 4.1.300 = 25
x = (35+5) : 2 = 20 ; x = 35 - 20 = 15
Vậy độ dài 2 góc vuông là 20cm và 15cm
BN
23 tháng 5 2016
Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25
độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)
Theo đề bài ta có pt :
x2 + (35 - x2) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0
\(\Delta=\left(-35\right)^2-4.1.300=25\)
x1 = (35+5) : 2 = 20 ; x2 = 35 - 20 = 15
Vậy độ dài 2 góc vuông là 20cm và 15cm
CM
7 tháng 9 2018
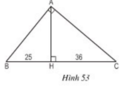
+ BC = BH + HC = 25 + 36 = 61 (cm)
+ ΔABH vuông tại H và ΔABC vuông tại A có:
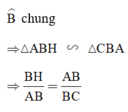
⇒AB2=BH.BC=25.(25+36)=1525
NT
1
9 tháng 2 2022
\(\Delta ABC\)vuông tại A nên \(AB^2+AC^2=BC^2\)(đl Py-ta-go)
Vì \(\Delta ABC\)vuông cân tại A nên \(AB=AC\)
Vậy \(2AB^2=BC^2\)hay \(\left(AB\sqrt{2}\right)^2=BC^2\)hay \(AB\sqrt{2}=BC\)hay \(AB=\frac{BC}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)
Như vậy \(AB=AC=\sqrt{2}\)
TT
2
VM
17 tháng 2 2017
ta có : ab^2 + bc^2 = ac^2
=> 20 + 60 =ac^2
=> 80 = ac^2
=> ac = 8,9
=> P abc = 20+60+8,9 =88,9 (cm)
Theo đề ta có: AB + AC + BC = 60 => AB + AC = 60 - 25 = 35 (1)
Theo Py-ta-go ta được: AB2 + AC2 = BC2 = 252 = 625 (2)
Từ (1) => AB = 35 - AC
Thay vào (2) ta được: (35 - AC)2 + AC2 = 625
=> 1225 - 70AC + AC2 + AC2 = 625
=> 2AC2 - 70AC + 600 = 0
=> AC = 20 hoặc AC = 15
+ Với AC = 20 => AB = 35 - 20 = 15
+ Với AC = 15 => AB = 35 - 15 = 20