Giúp tôi làm vài câu này với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
6
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2022
4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2022
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
11 tháng 6 2021
Phép lai 1:
Xét sự di truyền về màu sắc hạt ở F1 :
Vàng / Xanh = (45+16)/(15+5)= 3/1 (1)=> Vàng trội hơn xanh
Xét sự di truyền về hình dạng quả ở F1:
Trơn/Nhăn = 3/1 (2) => Trơn trội hơn nhăn
Quy ước gen :
Vàng A
Xanh a
Trơn B
Nhăn b
Từ (1) => Nghiệm đúng QLPL => P : Aa x Aa (3)
Từ (2) => Nghiệm đúng QLPL => P : Bb x Bb (4)
Kết hợp (3) và (4) => P : AaBb x AaBb
phép lai thứ 2 :
Xét sự di truyền về màu sắc hạt ở F1 :
Vàng/xanh = 1/1 => Nghiệm đúng phép lai phân tích => P : Aa x aa (1)
Xét sự di truyền về hình dạng quả ở F1:
Trơn/Nhăn = 1/1 => Nghiệm đúng phép lai phân tích => P : Bb x bb (2)
Từ (1) và (2) => P : Aabb x aaBb
N
14
H
16 tháng 12 2021
14. from -> since (HTHTTD nên dùng since)
15. with -> by (learn by heart: học thuộc lòng)
16. have been -> has been (Mathematics tuy có s ở cuối nhưng là số ít)
17. to wait -> waiting (mind Ving)
18. don't lock -> not to lock (told S to V/ not to V)
16 tháng 12 2021
14. from -> since
15. with -> by
16. have been -> has been
17. to wait -> waiting
18. don't lock -> not to lock
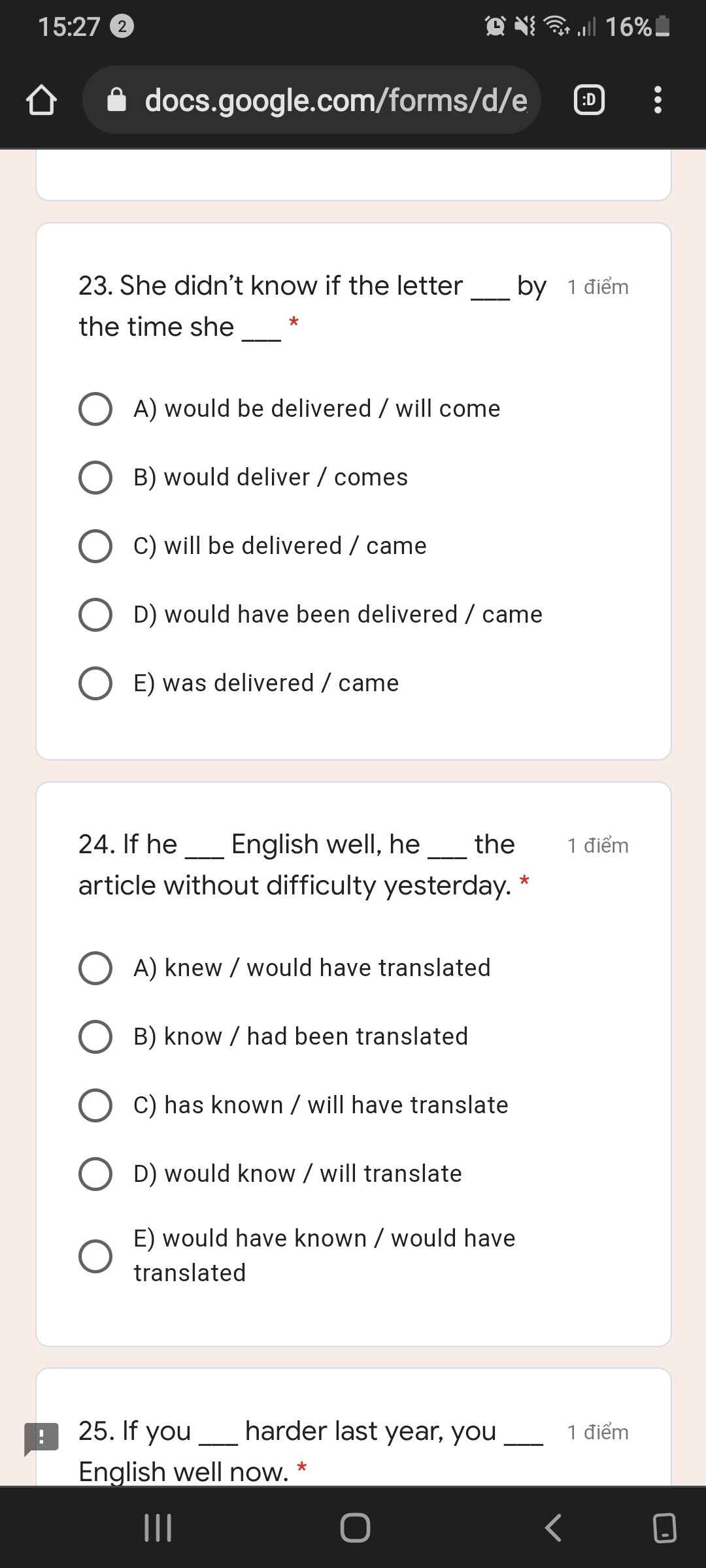
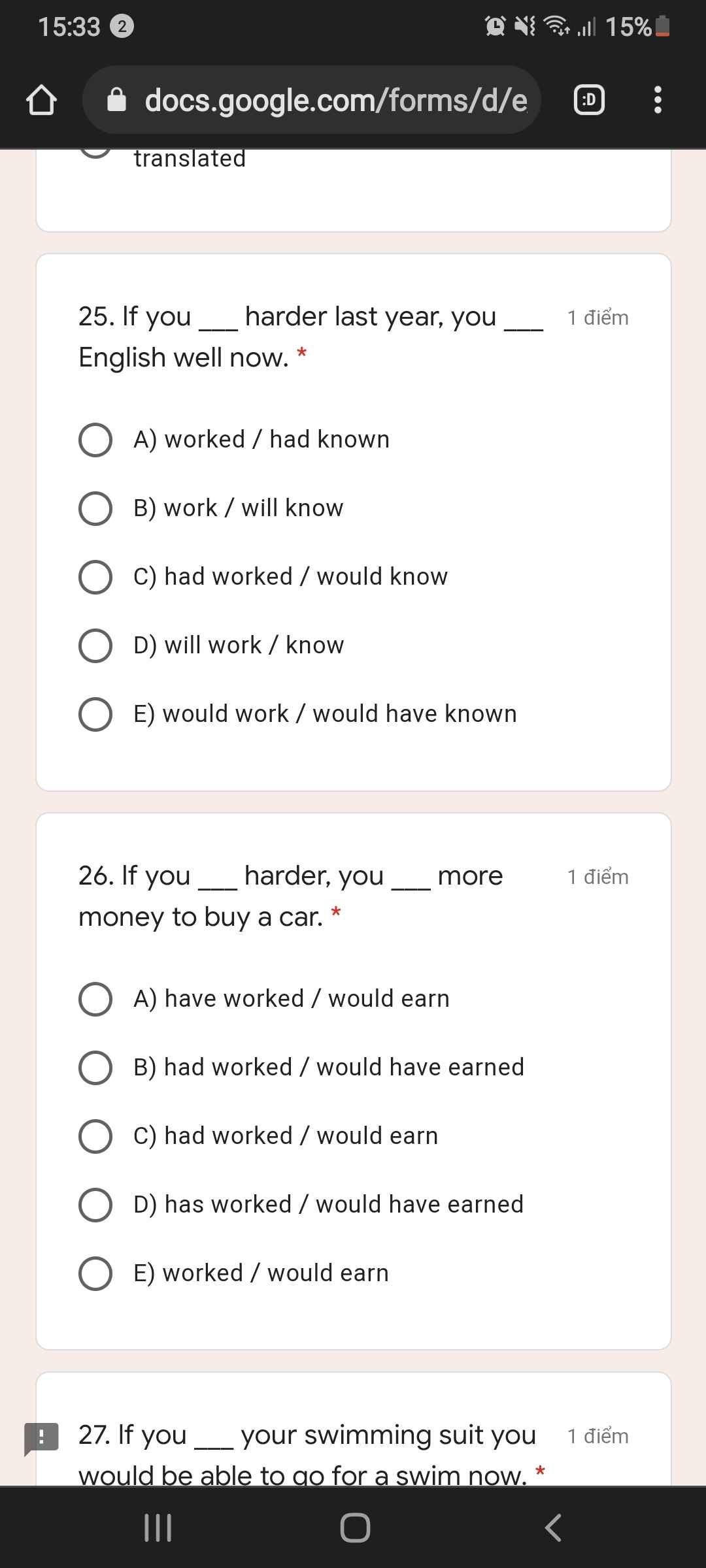
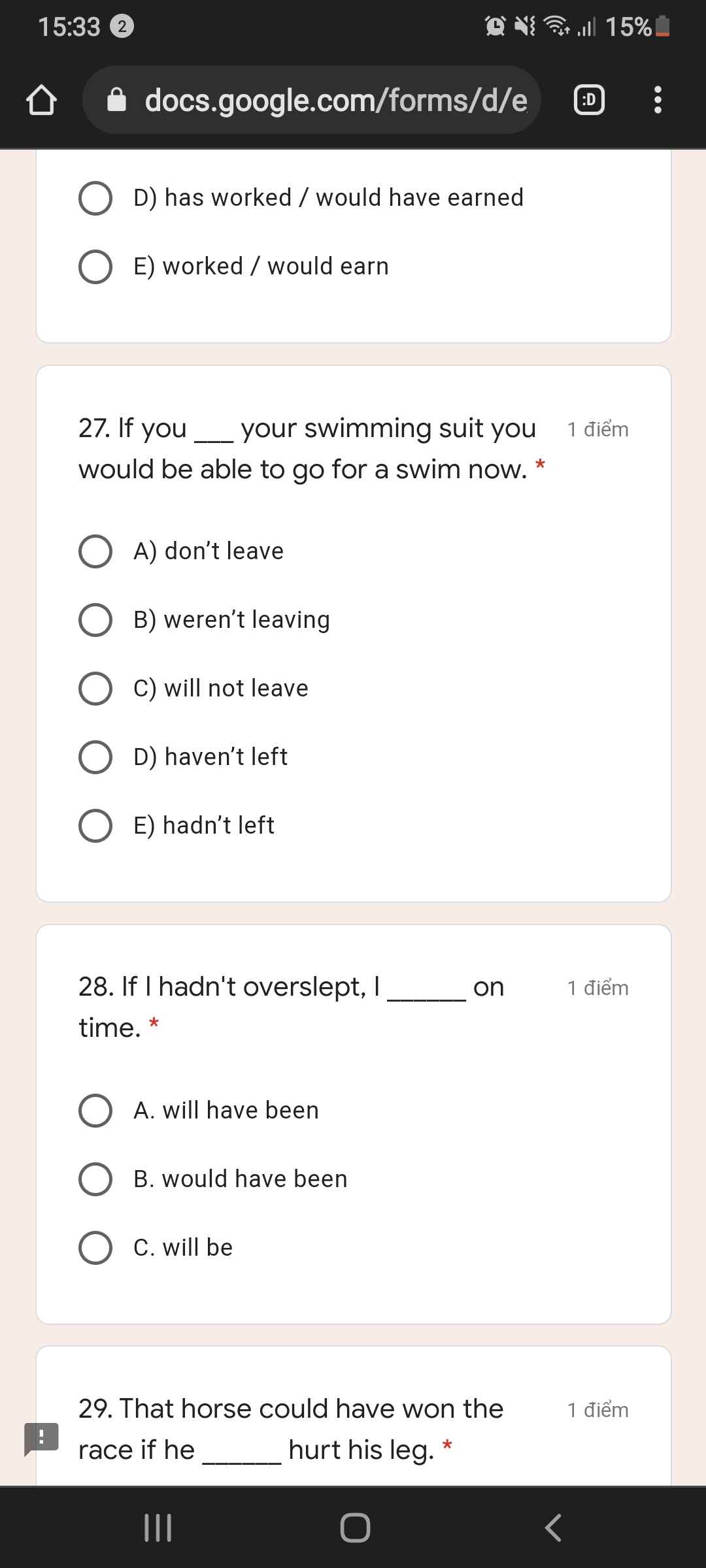
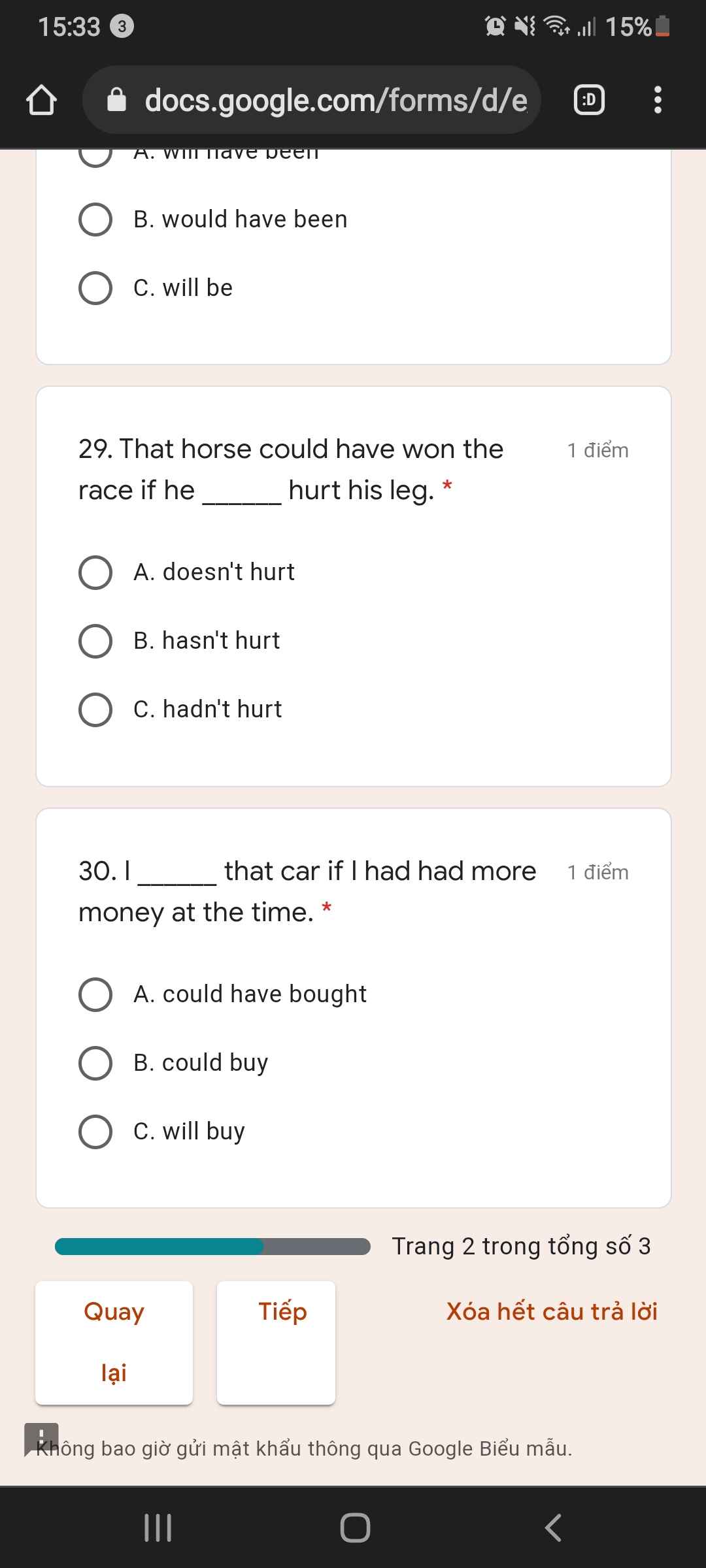
CÂU HỎI LÀ GÌ VẬY?????????????????????????
câu hỏi đâu