Cho $AB$ và $MN$ là hai đường kính khác nhau của đường tròn $(O)$. Tiếp tuyến tại $B$ của $(O)$ cắt các đường thẳng $AM$, $AN$ lần lượt tại $P$ và $Q$. Chứng minh:
a) $ABMN$ là hình chữ nhật.
b) Bốn điểm $M$, $N$, $P$, $Q$ cùng thuộc một đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: M,N,P,Q cùng thuộc một đường tròn
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>BM\(\perp\)AQ tại M
Xét (O) có
ΔBNA nội tiếp
BA là đường kính
Do đó: ΔBNA vuông tại N
=>BN\(\perp\)AP
Xét ΔABQ vuông tại B có BM là đường cao
nên \(AM\cdot AQ=AB^2\left(1\right)\)
Xét ΔABP vuông tại B có BN là đường cao
nên \(AN\cdot AP=AB^2\left(2\right)\)
Từ (1),(2) suy ra \(AM\cdot AQ=AN\cdot AP\)
=>\(\dfrac{AM}{AP}=\dfrac{AN}{AQ}\)
Xét ΔAMN và ΔAPQ có
\(\dfrac{AM}{AP}=\dfrac{AN}{AQ}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN đồng dạng với ΔAPQ
=>\(\widehat{AMN}=\widehat{APQ}\)
mà \(\widehat{AMN}+\widehat{QMN}=180^0\)(hai góc kề bù)
nên \(\widehat{QMN}+\widehat{QPN}=180^0\)
=>MNPQ là tứ giác nội tiếp
=>M,N,P,Q cùng thuộc một đường tròn

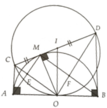
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

a) góc MAN nội tiếp chắn nửa (O) => góc MAN = 900 hay góc CAD = 900
tam giác CAD vuông tại A có đường cao AB => AM.AC = AB2 = 4R2 không đổi
b) Tam giác OAN có OA = ON = R nên cân tại O => góc OAN = góc ONA hay góc BAD = góc MNA
mà góc BAD = góc ACD (cùng phụ góc BAC) => góc MNA = góc ACD => tứ giác CMND nội tiếp
c) tam giác ACD vuông tại A có AI là trung tuyến => IA = ID = 1/2 CD => tam giác IAD cân tại I => góc IAD = góc IDA
mà góc IDA = góc AMN( tứ giác CMND nội tiếp) => góc IAD = góc AMN mà góc AMD phụ góc MNA => góc IAD phụ góc MNA
=> góc AHN = 900 hay góc AHO = 900 , mà OA = R không đổi => H nằm trên đường tròn đường kính AO
a﴿ góc MAN nội tiếp chắn nửa ﴾O﴿ => góc MAN = 90o hay góc CAD = 90o
tam giác CAD vuông tại A có đường cao AB => AM.AC = AB 2 = 4R 2 không đổi
b﴿ Tam giác OAN có OA = ON = R nên cân tại O => góc OAN = góc ONA hay góc BAD = góc MNA
mà góc BAD = góc ACD ﴾cùng phụ góc BAC﴿ => góc MNA = góc ACD => tứ giác CMND nội tiếp
c﴿ tam giác ACD vuông tại A có AI là trung tuyến => IA = ID = 1/2 CD => tam giác IAD cân tại I => góc IAD = góc IDA
mà góc IDA = góc AMN﴾ tứ giác CMND nội tiếp﴿
=> góc IAD = góc AMN mà góc AMD phụ góc MNA => góc IAD phụ góc MNA
=> góc AHN = 90 0 hay góc AHO = 90 0 , mà OA = R không đổi => H nằm trên đường tròn đường kính AO

Bài này cũng khó à nha ;)
a) ta có Góc ANB = 90° ( góc nội tiếp chắn nua đường tròn)
Và góc AMB = 90° (___________________________________)
Tương tự góc MAN = 90 (__________________________________)
=> Tứ giác AMBN là hình chữ nhật
B) Ta có Góc NAB = góc PBN ( cùng chắn cũng BN)
Mà Góc PBN + góc BPN = 90°
=> Góc NMB + Góc BPN = 90°
Tứ giác MNPQ có
Góc QMN+ góc BPN
= Góc QMB + góc NMB + Góc BPN
= 90 +90= 180°
=> Tứ giác MNPQ nội tiếp
Hãy M,N,P,Q cùng thuộc một đường tròn
C) ko bt làm
D) MN vuông góc AB nha do vộ quá nên ko viết đc bạn cứ kẻ đường cao rồi chứng minh
Cho ABAB và MNMN là hai đường kính khác nhau của đường tròn (O)(O). Tiếp tuyến tại BB của (O)(O) cắt các đường thẳng AMAM, ANAN lần lượt tại PP và QQ. Chứng minh:
a) ABMNABMN là hình chữ nhật.
b) Bốn điểm MM, NN, PP, QQ cùng thuộc một đường tròn.
a) Theo gt, ta có :
ABAB và MNMN là hai đường kính khác nhau của đường tròn (O)(O)
=> góc MAN= MBN=AMB=ANB (tính chất góc nội tiếp nhìn nửa đường tròn)
=> AMBN là hình chữ nhật (đpcm)
b) Ta thấy:
MNA= MBA (cùng chắn cung MA)
MBA= 90 - PAB (tính chất tổng 3 góc trong tam giác MBA)
MPB= 90 - PAB (tính chất tổng 3 góc trong tam giác MPB)
=> MNA = MPA => đpcm (vì là tứ giác có góc ngoài tam giác bằng góc đối trong tứ giác)