cho tam giác ABC nội tiếp đường tròn (O), M là điểm di chuyển trên đường tròn. Gọi H,K là hình chiếu của M trên BA,BC. Xác định vị trí của M để độ dài HK đạt GTLN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2017
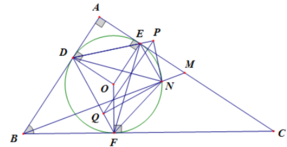
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.
8 tháng 4 2020
Ta có nếu R là bán kính đường tròn nội tiếp của 1 tam giác đều cạnh a thì: \(R=\frac{a\sqrt{3}}{3}\) (*)
Dựng 2 tam giác đều BDF và tam giác CDG về phía ngoài tam giác ABC, khi đó \(\widehat{BFD}=\widehat{BED}=60^o\); \(\widehat{CGD}=\widehat{CED}=60^o\)
=> BDEF và CDEG là các tứ giác nội tiếp
Nên R1;R2 lần lượt là bán kính của các đường tròn ngoại tiếp các \(\Delta\) đều BDF và CDG
Theo (*) ta có: \(\hept{\begin{cases}R_1=\frac{BD\sqrt{3}}{3}\\R_2=\frac{CD\sqrt{3}}{3}\end{cases}\Rightarrow R_1R_2=\frac{BD\cdot CD}{3}}\)
Mặt khác \(\left(BD+CD\right)^2=4\cdot BD\cdot CD\)
\(\Rightarrow BD\cdot CD\le\frac{\left(BD+CD\right)^2}{4}=\frac{BC^2}{4}=\frac{3R^2}{4}\Rightarrow R_1R_2\le\frac{R^2}{4}\)
Đẳng thức xảy ra khi BD=CD