Bài 5. Cho góc xOy khác góc bẹt, Oz là tia phân giác. Từ điểm M bất kì trong góc xOz kẻ
MH ⊥ Ox,(H ∈Ox) , MK ⊥ Oy,(K ∈Oy) . Gọi N là giao điểm của MK với Oz. Từ N kẻ
NP ⊥ Ox .
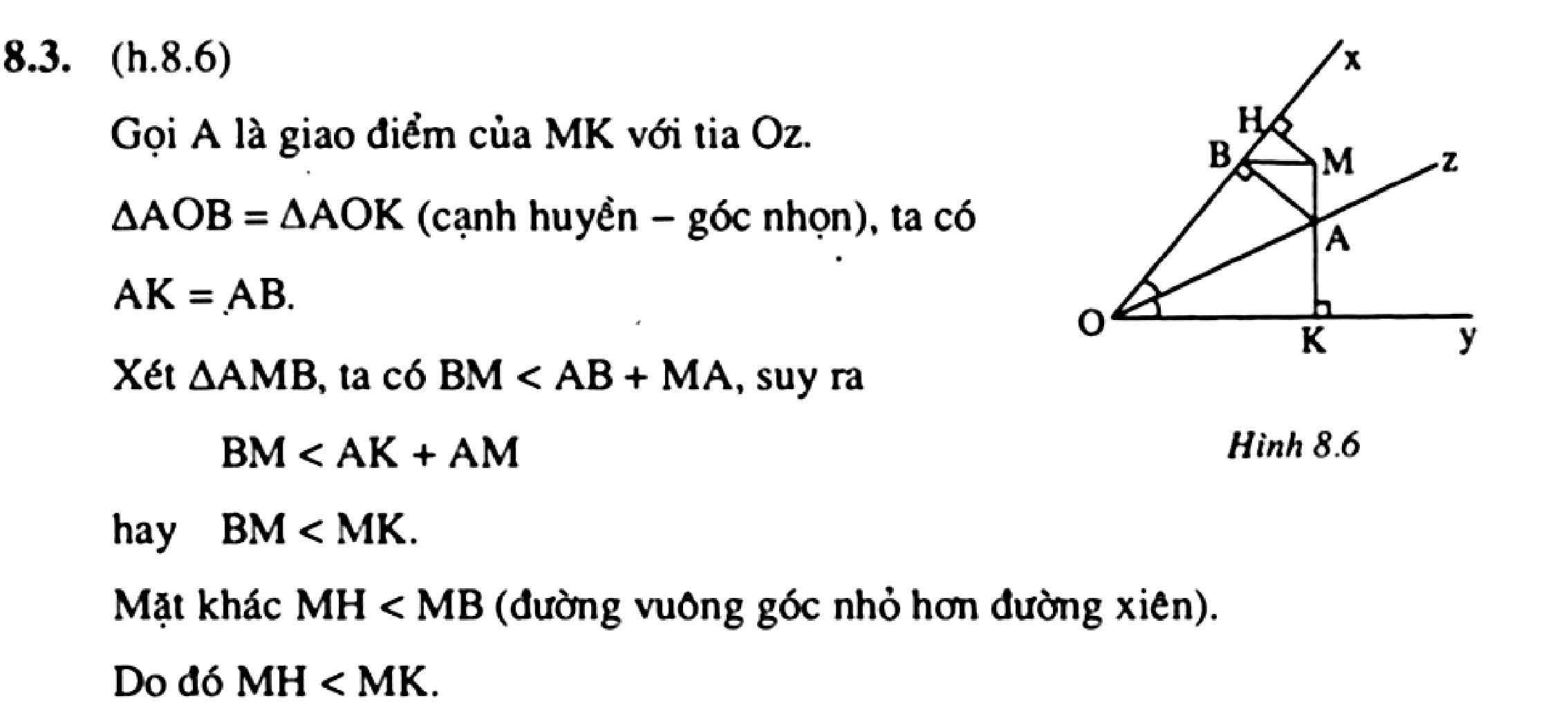
a) Chứng minh PM<MK
b) Chứng minh MH<MK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 4 2023
góc BMO=góc HOK=góc BOM
=>ΔBMO cân tại B
=>K là trung điểm của OM
=>OK=KM
Xet ΔHOB vuông tại H và ΔKBO vuông tại K có
BO chung
góc HOB=góc KBO
=>ΔHOB=ΔKBO
=>OK=BH=MK
24 tháng 4 2020
a) Xét \(\Delta OMH\)và \(\Delta OMK\)có :
OM chung
\(\widehat{O_1}=\widehat{O_2}\)( do Oz là tia phân giác của ^xOy )
=> \(\Delta OMH=\Delta OMK\)( cạnh huyền - góc nhọn )
=> \(MH=MK\)( hai cạnh tương ứng )
b) Từ \(\Delta OMH=\Delta OMK\)=> \(OH=OK\)( hai cạnh tương ứng )
Xét \(\Delta MBK\)và \(\Delta MAH\)có :
\(MB=MA\)( gt )
\(MH=MK\)( cmt )
=> \(\Delta MBK=\Delta MAH\)( cạnh huyền - cạnh góc vuông )
=> \(BK=AH\)( hai cạnh tương ứng )
Ta có : \(OH=OA+AH\)
\(OK=OB+BK\)
mà OH = OK ; AH = BK
=> OA = OB ( đpcm )