Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn kiểm tra lại đề từ chỗ M là điểm bất kì nằm trên Ox đến hểt

Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)

a) Ta có :
O1 = O2
Vì AM // Oy
=> O1 = O2 = M1 = M2 (cặp góc sole )
Xét 2 tam giác OAM và tam giác OBM , có :
O1 = O2
OM là cạnh chung => tam giác OAM = tam giác OBM (g.c.g)
M1 = M2
=> OA = OB ; MA = MB
b) Xét 2 tam giác vuông OHM và OKM có :
O1 = O2
OM chung
=> tam giác OHM = tam giác OKM (theo trường hợp Cạnh huyền góc nhọn)
=> MH = MK

Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
Suy ra: MA=MB
Xét ΔOKM vuông tại K và ΔOHM vuông tại H có
OM chung
\(\widehat{KOM}=\widehat{HOM}\)
Do đó;ΔOKM=ΔOHM
Suy ra: OH=OK
=>AH=BK
Xét ΔMAH vuông tại H và ΔMBK vuông tại K có
MA=MB
AH=BK
Do đó: ΔMHA=ΔMKB

A .
Vì OA // MB ( giả thuyết )
=> Góc AOM = Góc OMB ( 1 )
Vì AM = OB ( giả thuyết )
=> Góc AMO = Góc MOB ( 2 )
Từ ( 1 ) và ( 2 )
=> Góc AOM = Góc MOB ; Góc AMO = Góc BMO
Vậy hình tam giác AMO = Hình tam giác BMO ( góc - cạnh - góc )
= > AO = OB ; MA = MB ( 2 cạnh tương ứng )
Đề thấy sai sai!!
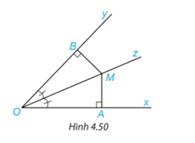
a) Xét \(\Delta OMH\)và \(\Delta OMK\)có :
OM chung
\(\widehat{O_1}=\widehat{O_2}\)( do Oz là tia phân giác của ^xOy )
=> \(\Delta OMH=\Delta OMK\)( cạnh huyền - góc nhọn )
=> \(MH=MK\)( hai cạnh tương ứng )
b) Từ \(\Delta OMH=\Delta OMK\)=> \(OH=OK\)( hai cạnh tương ứng )
Xét \(\Delta MBK\)và \(\Delta MAH\)có :
\(MB=MA\)( gt )
\(MH=MK\)( cmt )
=> \(\Delta MBK=\Delta MAH\)( cạnh huyền - cạnh góc vuông )
=> \(BK=AH\)( hai cạnh tương ứng )
Ta có : \(OH=OA+AH\)
\(OK=OB+BK\)
mà OH = OK ; AH = BK
=> OA = OB ( đpcm )