giải bài 14,15,16,19,28,38,41 sách bài tập giúp mik nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bàu 68:
-Các t/c đó đc suy ra từ các định lý:
+a,b)định lý:Tổng ba góc của một tam giác bằng 180°
+c)đl:Trong một tam giác cân,hai góc ở đáy = nhau
+d)đl:Nếu một tam giác có hai góc =nhau thì tam giác đó là tam giác cân
HÙGHJUJNHJRJIJKJHJUIRGJUIJUIGJUIGJUIFKJIOJUITJUIKIOUJRJUIGJUTRGJUI6JUHJUIHJYUIJUIGJUIJUIRIGIJUIERGJU6JIGJUIJUITGHJUTJUIHITGJUIYIJH

bạn vào đây,Chương trình toán lớp 6, lý thuyết công thức toán SGK lớp 6, muốn bài nào , có bài đó


Bài 71 :
Tam giác AHB = tam giác CKA ( c . g . c )
=> AB = CA , tam giác BHA = tam giác ACK
Ta lại có : Tam giác ACK + tam giác CAK = 90 độ
Nên tam giác BAH + tam giác CAK = 90 độ
Do đó tam giác BAC = 90 độ
Vậy tam giác ABC là tam giác vuông tại A
Bài 72
Xếp tam giác đều : Xếp tam giác với mỗi cạnh là bốn que diêm
Một tam giác cân mà ko đều : 2 cạnh bên 5 que diêm , cạnh đáy 2 que
Xét tam giác vuông : xếp tam giác có cạnh lần lượt là : ba , bốn , năm que diêm
Bài 73 ;
So sánh AC + CD vào 2 x BA
+ Xét tam giác AHB vuông tại H ,ta có :
AB2 = AH2 + HB2 ( định lý PItago )
=> HB2 =AB2 - AH2
=> HB2 = 5 - 3 = 25 - 9 =16 ( định lý Pitago )
=> HB= 4 ( vì HB > 0 )
+ Vì H nằm giữa B và C => :
HC = BC - HB = 10 - 4 = 6
+ Xét tam giác AHC vuông tại H , ta có
AC = AH + HC ( ĐỊNH LÝ PITAGO )
AC = 3 + 6 = 9 + 36 = 45
=> AC = 45 ( vì AC > 0 )
hay AC = 6,71

"Cố hương" là tác phẩm nổi tiếng của nhà văn Lỗ Tấn.Trong truyện ngắn này,thông qua việc thuật lại chuyến về quê lần cuối của nhân vật "tôi",tác giả đã bày tỏ nhưng rung động trước những thay đổi của làng quên đặc biệt là Nhuận Thổ-1 người bạn đã gắn bó vs tuổi thơ "tôi"
2.Những thay đổi của Nhuận Thổ:
a/Hình dáng:
*20năm trước:khuôn mặt tròn trĩnh,nước da bánh mật,khỏe mạnh.
*20năm sau:cao gấp 2 lần trước,da vàng sạm,mắt húp đỏ mọng lên,bàn tay nứt nẻ như vỏ cây thông.
b/Ăn mặc:
*Trước:đội mũ lông chiên bé tí tẹo,cổ đeo vòng bạc
*Sau:Đội mũ lông chiên rách tươm,mặc áo bông mỏng dính
c/Nói năng:
*Trước:tự tin,rõ ràng,trong trẻo.
*Sau:nói ko ra tiếng,khách sáo,giữ khoảng cách.
d/Thái độ:
*Trước:nhanh nhẹn,dũng cảm,khỏe khoắn,hoạt bát
*Sau:co ro,cúm rúm,cung kính,thê lương,sợ sệt,lễ phép.
e/Tính cách:
*Trước:Giàu tình cảm,hồn nhiên,chân thật,chân thành.
*Sau:Sợ sệt,luôn giữ khoảng cách,cam chịu rụt rè.
3.Nêu tư tưởng của tác giả:
Với sự thay đổi của nhân vật Nhuận Thổ,Lỗ Tấn đã phê phán xã hội phong kiến,lễ giáo phong kiến,đặt ra vấn đề đường đi của nông dân và toàn xã hội để mọi người suy ngẫm.

Câu 26 trang 89 Sách Bài Tập (SBT) Toán Lớp 6 tập 2
So sánh hai góc ở hình 10.
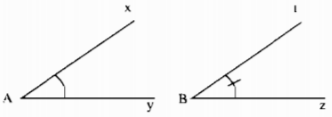
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
Giải
Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.
Tính tổng số đo hai góc trên hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.
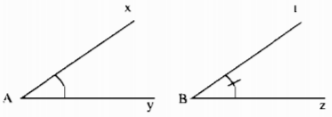
Giải
Sử dụng thước đo độ sau đó cộng số đo hai góc.
a) Vẽ góc có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí \(M_1\). Đặt mẫu hình nhiều lần để được nhiều vị trí \(M_1,M_2,M_3\).. khác nhau của đỉnh M. Vậy ta có:
\(\widehat{AM_1B}=\widehat{AM_2B}=\widehat{AM_3B}=...=40^o\)
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)

Giải
b) Quỹ đạo của điểm M được gọi là "cung chứa góc \(40^o\)
Bài 29 tự làm,có trong sách mà bạn
Bài 26 trang 89 Toán 6
So sánh hai góc ở hình 10.

Hướng dẫn: Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
Giải: Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.
Bài 27 trang 89
Tính tổng số đo hai góc trên hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.

Giải: Sử dụng thước đo độ sau đó cộng số đo hai góc.
Bài 28 Toán 6
a) Vẽ góc có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí M1M1. Đặt mẫu hình nhiều lần để được nhiều vị trí M1,M2,M3M1,M2,M3, … khác nhau của đỉnh M. Vậy ta có:
ˆAM1B=ˆAM2B=ˆAM3B=…=400AM1B^=AM2B^=AM3B^=…=400
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)

HD: b) Quỹ đạo của điểm M được gọi là “cung chứa góc 400400.
29a) Ta có hình vẽ

b) Vì ˆARNARN^ và ˆSRNSRN^ kề bù nên:
ˆARN+ˆSRN=180OARN^+SRN^=180O
Thay ˆSRN=130OSRN^=130O ta có:
ˆARN+130O=180OARN^+130O=180O
⇒ˆARN=180O–130O=50O⇒ARN^=180O–130O=50O
Vì ˆARMARM^ và ˆMRSMRS^ kề bù nên:
ˆARM+ˆMRS=180OARM^+MRS^=180O
Thay ˆARM=130OARM^=130O ta có:
130O+ˆMRS=180O130O+MRS^=180O
⇒ˆMRS=180O–130O=50O⇒MRS^=180O–130O=50O
Vì hai tia RN và RM nằm trên cùng môt nửa mặt phẳng bờ chứa tia RA
ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O suy ra ˆARN<ˆARMARN^<ARM^
Nên tia RN nằm giữa hai tia RA và RM
⇒ˆARN+ˆMRN=ˆARM⇒ARN^+MRN^=ARM^. Thay ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O ta có:
50O+ˆMRN=130O50O+MRN^=130O
⇒ˆMRN=130O–50O=80O

số nước cần phải đổ vào bể để bể đầy là
\(1-\frac{3}{4}=\frac{1}{4}\)(bể)
khi mở vòi nước thì số thời gian bể sẽ đầy là \(\frac{1}{4}:\frac{1}{8}=2\)(giờ)
vậy....
12.5* gọi hai số đó là a và b
ta có:a-b=9 (1)
\(\frac{7}{9}a=\frac{28}{33}b\)
=> \(a=\frac{28}{33}b:\frac{7}{9}\)
\(=>a=\frac{12}{11}b\)(2)
thay (2) vào (1) ta đc
\(\frac{12}{11}b-b=9\)
=> \(\frac{1}{11}b=9\)
=>b=99
=> a=99+9=108
vậy...