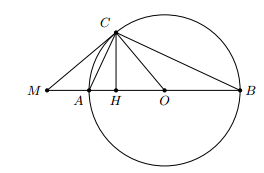
Cho nửa đường tròn $(O)$ đường kính $AB$. Trên tia đối của tia $AB$ lấy một điểm $M$. Vẽ tiếp tuyến $MC$ với nửa đường tròn. Gọi $H$ là hình chiếu của $C$ trên $AB$.
a) Chứng minh rằng $CA$ là tia phân giác của góc $MCH$.
b) Giả sử $MA = a$, $MC = 2a$. Tính \(AB\) và $CH$ theo $a$.





ta có góc ACH=gócABC(vì cùng phụ với góc CAB)
MCA=ABC(vì cùng chắn cung AC)
=> góc MCA=ACH hay AC là tia phân giác của góc MCH