Tìm tập nghiệm của phương trình:
(x-1)-(5x+4)+5x(x-2)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 10 2021
\(a,ĐK:x\ge\dfrac{1}{5}\\ PT\Leftrightarrow5x-1=64\\ \Leftrightarrow x=13\left(tm\right)\\ b,ĐK:x\ge\dfrac{2}{5}\\ BPT\Leftrightarrow5x-2< 16\\ \Leftrightarrow x< \dfrac{18}{5}\\ \Leftrightarrow\dfrac{2}{5}\le x< \dfrac{18}{5}\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\left|x-1\right|-\left|x-2\right|=x-3\\ \Leftrightarrow\left[{}\begin{matrix}1-x-\left(2-x\right)=x-3\left(x< 1\right)\\x-1-\left(2-x\right)=x-3\left(1\le x< 2\right)\\x-1-\left(x-2\right)=x-3\left(x\ge2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=0\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
CM
4 tháng 10 2019
Ta có: 5x – 2(4- x) >0
⇔ 5 x - 8 + 2 x > 0 ⇔ 7 x > 8 ⇔ x > 8 7
Tập nghiệm của bất phương trình đã cho là: S = 8 7 ; + ∞
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
LA
3 tháng 5 2022
1.
xét delta có
25 -4(-m-3)
= 25 + 4m + 12
= 4m + 37
để phương trình có nghiệm kép thì delta = 0
=> 4m + 37 = 0 => m = \(\dfrac{-37}{4}\)
2.
a) xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có nghiệm kép thì delta = 0
=> -4m + 37 = 0
=> m = \(\dfrac{37}{4}\)
b)
xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có 2 nghiệm phân biệt thì delta > 0
=> -4m + 37 > 0
=> m < \(\dfrac{37}{4}\)
CM
28 tháng 10 2019
Đáp án A
Điều kiện x ≥ − 2
Đặt t = x + 2 t ≥ 0 ⇒ x = t 2 − 2
Khi đó phương trình tương đương
5 − t 2 + t + 2 − 5 m = 0 ⇔ m = 5 − t 2 + t + 1
Xét hàm số f t = 5 − t 2 + t + 1 ; t ≥ 0.
Ta có:
f ' t = − 2 t + 1 5 − t 2 + t + 1 ; f ' t = 0 ⇔ t = 1 2
Từ bảng biến thiên ra suy ra phương trình có nghiệm thì 0 < m ≤ 5 5 4
CM
29 tháng 6 2018
Đáp án A
Điều kiện x ≥ 2
Đặt t = x + 2 t ≥ 0 ⇒ x = t 2 - 2
Khi đó phương trình tương đương
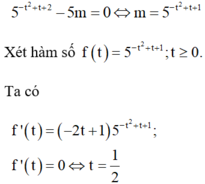
Từ bảng biến thiên ra suy ra phương trình có nghiệm thì 0 < m < 5 5 4 .
\(\Leftrightarrow x-1-5x-4+5x^2-10x=0\)
\(\Leftrightarrow5x^2-14x-5=0\)
\(\text{Δ}=\left(-14\right)^2-4\cdot5\cdot\left(-5\right)=296>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{14-2\sqrt{74}}{10}=\dfrac{7-\sqrt{74}}{5}\\x_2=\dfrac{7+\sqrt{74}}{5}\end{matrix}\right.\)
\(\left(x-1\right)-\left(5x+4\right)+5x\left(x-2\right)=0\\ \Leftrightarrow x-1-5x-4+5x^2-10x=0\\ \Leftrightarrow5x^2-14x-5=0\)
\(\Delta=\left(-14\right)^2-4.5.\left(-5\right)=196+100=296\)
\(x_1=\dfrac{-\left(-14\right)+\sqrt{296}}{2.5}=\dfrac{14+2\sqrt{74}}{10}=\dfrac{7+\sqrt{74}}{5}\)
\(x_2=\dfrac{-\left(-14\right)-\sqrt{296}}{2.5}=\dfrac{14-2\sqrt{74}}{10}=\dfrac{7-\sqrt{74}}{5}\)