Em xin lời giản con b bài 1 với con b bài 2 ạ em cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TP
2
Những câu hỏi liên quan
AN
2
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 8 2021
Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 11 2023
Olm chào em. Cảm ơn em đã tin tưởng và đồng hành cùng olm trong suốt thời gian qua. Với dạng này em làm như sau nhé:
Gọi số học sinh của khối đó là \(x\) (học sinh) 0 < \(x\) < 300; \(x\) \(\in\) N
Theo bài ra ta có: ( \(x\) + 2) \(⋮\) 4; 5; 6
⇒ (\(x\) + 2) \(\in\) BC(4; 5; 6)
4 = 22; 5 = 5; 6 = 2.3 ⇒ BCNN(4; 5;6) = 22.3.5 = 60
⇒ BC(4;5;6) = {0; 60; 120; 180; 240; 300; 360; 420; ...;}
Vì 0< \(x\) < 300 ⇒0< \(x\) + 2 < 300 + 2 ⇒ 2 < \(x\) + 2 < 302
⇒ \(x\) + 2 \(\in\){60; 120; 180; 240; 300}
Lập bảng ta có:
| \(x+2\) | 60 | 120 | 180 | 240 | 300 |
| \(x\) | 58 | 118 | 178 | 238 | 298 |
Vậy \(x\) \(\in\){58; 118; 178; 238; 298}
14 tháng 11 2023
Gọi số học sinh của khối đó là (học sinh) 0 < < 300; N
Theo bài ra ta có: ( + 2) 4; 5; 6
⇒ ( + 2) BC(4; 5; 6)
4 = 22; 5 = 5; 6 = 2.3 ⇒ BCNN(4; 5;6) = 22.3.5 = 60
⇒ BC(4;5;6) = {0; 60; 120; 180; 240; 300; 360; 420; ...;}
Vì 0< < 300 ⇒0< + 2 < 300 + 2 ⇒ 2 < + 2 < 302
⇒ + 2 {60; 120; 180; 240; 300}
Lập bảng ta có:
| 60 | 120 | 180 | 240 | 300 | |
| 58 | 118 | 178 | 238 | 298 |
Vậy {58; 118; 178; 238; 298}
TN
1
CM
3
14 tháng 12 2023
Ngọc Hoàng thấu hiểu khó khăn của người dân và tìm cách giúp dân. Một hôm ngài triệu một vị thần đến giao cho hai bao hạt: bao màu đỏ là hạt ngũ cốc, bao màu xanh là hạt cỏ cây. Vị thần ấy phải mang xuống hạ giới và nhớ kĩ lời ta, gieo hết bao ngũ cốc màu đỏ trên phần lớn mặt đất để dân chúng lấy lương thực ăn. Còn lại một phần nhỏ đất đai thì gieo một ít hạt cỏ cây để tô điểm cho đồng ruộng và làm thức ăn cho các loài vật. Song trên đường đi vị thần ấy lại mải chơi nên quên mất khiến người dân dù có lương thực để ăn nhưng phải nhổ cỏ rất cực nhọc. Ngọc Hoàng quyết định phạt vị thần ấy hoá kiếp thành con vật có tên là Trâu, suốt đời sẽ phải kéo cày cho nông dân làm đất trồng ngô lúa hoa mầu. Từ đó, Trâu đã trở thành bạn của nhà nông, và đã được người nông dân yêu mến, tôn vinh là " Đầu cơ nghiệp "
10 tháng 7 2021
1. English is more interesting than music.
2. Today they are not as happy as they were yesterday.
3. Ha Noi is not as small as Hai Duong.
4. Mai's sister is not as pretty as her.
6. You have got more money than me.
7. Art is not as difficult as French.
8. Nam's father is more careful than him.
9. No one in our town is as rich as Mr Ron.
10. He is the most intelligent in my class.
11. Everest is the highest mountain in the world.
12. Minh is the fattest person in my group.
13. I can't swim as far as Jan.
14B 15C 16A 17C 18B 19C 20B
NL
1
17 tháng 10 2021
Bài 7:
a: \(A=x+\sqrt{x}\ge0\forall x\)
Dấu '=' xảy ra khi x=0
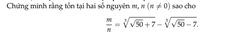
thầy nguyễn việt lâm ko onl thì chịu:<
1b/ \(\overrightarrow{AB}=\left(1;1;3\right);\overrightarrow{u_{Oy}}=\left(0;1;0\right)\)
Vì \(\left(P_2\right)//AB//Oy\Rightarrow\overrightarrow{n_{\left(P_2\right)}}=\left[\overrightarrow{AB},\overrightarrow{u_{Oy}}\right]=\left(\left|\begin{matrix}1&3\\1&0\end{matrix}\right|,\left|\begin{matrix}3&1\\0&0\end{matrix}\right|,\left|\begin{matrix}1&1\\0&1\end{matrix}\right|\right)=\left(-3;0;1\right)\)
\(\Rightarrow\left(P_2\right):-3\left(x+3\right)+z-5=0\Leftrightarrow\left(P_2\right):3x-z+14=0\)
2b/
\(\overrightarrow{u_{Ox}}=\left(1;0;0\right);\overrightarrow{n_{\left(Q\right)}}=\left(3;2;5\right)\)
\(\Rightarrow\overrightarrow{n_{\left(\beta\right)}}=\left[\overrightarrow{u_{Ox}},\overrightarrow{n_{\left(Q\right)}}\right]=\left(0;-5;2\right)\)
\(d\left(O,\left(\beta\right)\right)=\dfrac{\left|d\right|}{\sqrt{25+4}}=\sqrt{29}\Rightarrow d=\pm29\)
\(\Rightarrow\left[{}\begin{matrix}\left(\beta\right):-5y+2z+29=0\\\left(\beta\right):-5y+2z-29=0\end{matrix}\right.\)