Tìm x,y thoả mãn phương trình sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left(x^2-6x+9\right)+\left(y^2-4y+4\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(y-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left(y-2\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)

đến h vẫn còn ôn thi à
\(x^2-4x+y^2-6y+15=2\)
\(< =>\left(x^2-4x+4\right)+\left(y^2-6y+9\right)=0\)
\(< =>\left(x-2\right)^2+\left(y-3\right)^2=0\)
Do \(\left(x-2\right)^2\ge0;\left(y-3\right)^2\ge0\)
\(=>\left(x-2\right)^2+\left(y-3\right)^2\ge0\)
Dấu "=" xảy ra \(< =>\hept{\begin{cases}x=2\\y=3\end{cases}}\)

Bài 1: Bài này số nhỏ nên chỉ cần chặn miền giá trị của \(x\) rồi xét các trường hợp thôi nhé. Ta thấy \(3^x< 35\Leftrightarrow x\le3\). Nếu \(x=0\) thì \(VT=2\), vô lí. Nếu \(x=1\) thì \(VT=5\), cũng vô lí. Nếu \(x=2\) thì \(VT=13\), vẫn vô lí. Nếu \(x=3\) thì \(VT=35\), thỏa mãn. Vậy, \(x=3\).
Bài 2: Nếu \(x=0\) thì pt đã cho trở thành \(0!+y!=y!\Leftrightarrow0=1\), vô lí,
Nếu \(x=y\) thì pt trở thành \(2x!=\left(2x\right)!\) \(\Rightarrow\left(x+1\right)\left(x+2\right)...\left(2x\right)=2\) \(\Leftrightarrow x=1\Rightarrow y=1\)
Nếu \(x\ne y\) thì không mất tính tổng quát, giả sử \(1< y< x\) thì \(x!+y!< 2x!\le\left(x+1\right)x!=\left(x+1\right)!< \left(x+y\right)!\) nên pt đã cho không có nghiệm trong trường hợp này.
Như vậy, \(x=y=1\)
Bài 3: Bổ sung đề là pt không có nghiệm nguyên dương nhé, chứ nếu nghiệm nguyên thì rõ ràng \(\left(x,y\right)=\left(0,19\right)\) là một nghiệm cũa pt đã cho rồi.
Giả sử pt đã cho có nghiệm nguyên dương \(\left(x,y\right)\)
Khi đó \(x,y< 19\). Không mất tính tổng quát ta có thể giả sử \(1< y\le x< 19\). Khi ấy \(x^{17}+y^{17}=19^{17}\ge\left(x+1\right)^{17}=x^{17}+17x^{16}+...>x^{17}+17x^{16}\), suy ra \(y^{17}>17x^{16}\ge17y^{16}\) \(\Rightarrow y>17\). Từ đó, ta thu được \(17< y\le x< 19\) nên \(x=y=18\). Thử lại thấy không thỏa mãn.
Vậy pt đã cho không có nghiệm nguyên dương.

Từ hệ được x+y=1
a)Thay vào được x=1;y=0
b)Với mọi a
c)Thay vào x+y=1 tìm x;y
Thay ngược vào hệ tìm a
a) Khi a = 2 hệ phương trình đã cho tương đương với:
\(\hept{\begin{cases}x+2x=3\left(1\right)\\2x-y=2\left(2\right)\end{cases}}\Leftrightarrow\hept{\begin{cases}3x=3\\2x-y=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\2x-2=y\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\2.1-2=0=y\end{cases}}\)
Do vậy \(\left(x;y\right)=\left(1;0\right)\)
b) Ta có: \(x+y=\left(x+ax\right)-\left(ax-y\right)=3-2=1>0\forall a\)
c) Lấy (1) trừ (2),vế với vế,ta có: \(x+y=1\)
Thay vào,ta có: \(\sqrt{2}.y+y=1\Leftrightarrow y\left(\sqrt{2}+1\right)=1\)
\(\Rightarrow y=\frac{1}{\sqrt{2}+1}\Rightarrow x=1-\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}}{\sqrt{2}+1}\)
Thay vào hệ phương trình ban đầu,ta có: \(\hept{\begin{cases}\frac{\sqrt{2}}{\sqrt{2}+1}+\frac{\sqrt{2}}{\sqrt{2}+1}.a=3\left(3\right)\\\frac{\sqrt{2}}{\sqrt{2}+1}.a-\frac{\sqrt{1}}{\sqrt{2}+1}=2\left(4\right)\end{cases}}\)
Lấy (3) + (4),vế với vế,ta có: \(\frac{2\sqrt{2}}{\sqrt{2}+1}.a=5\Leftrightarrow a=\frac{10+5\sqrt{2}}{4}\)


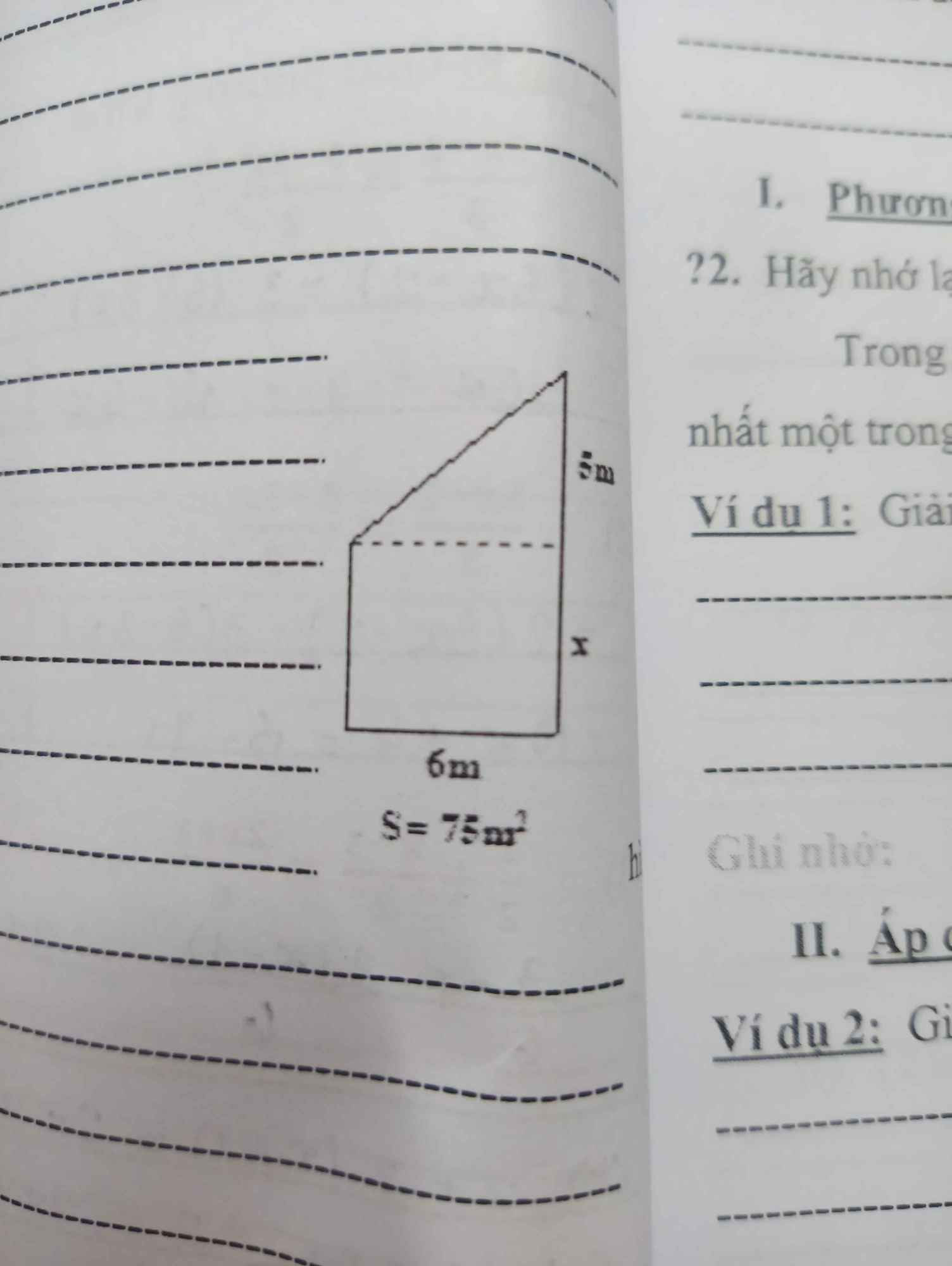
\(6.\left(5+x\right)=75\)
\(30+6x=75\)
\(6x=75-30=45\)
\(\Rightarrow x=\dfrac{45}{6}=7,5\left(cm\right)\)

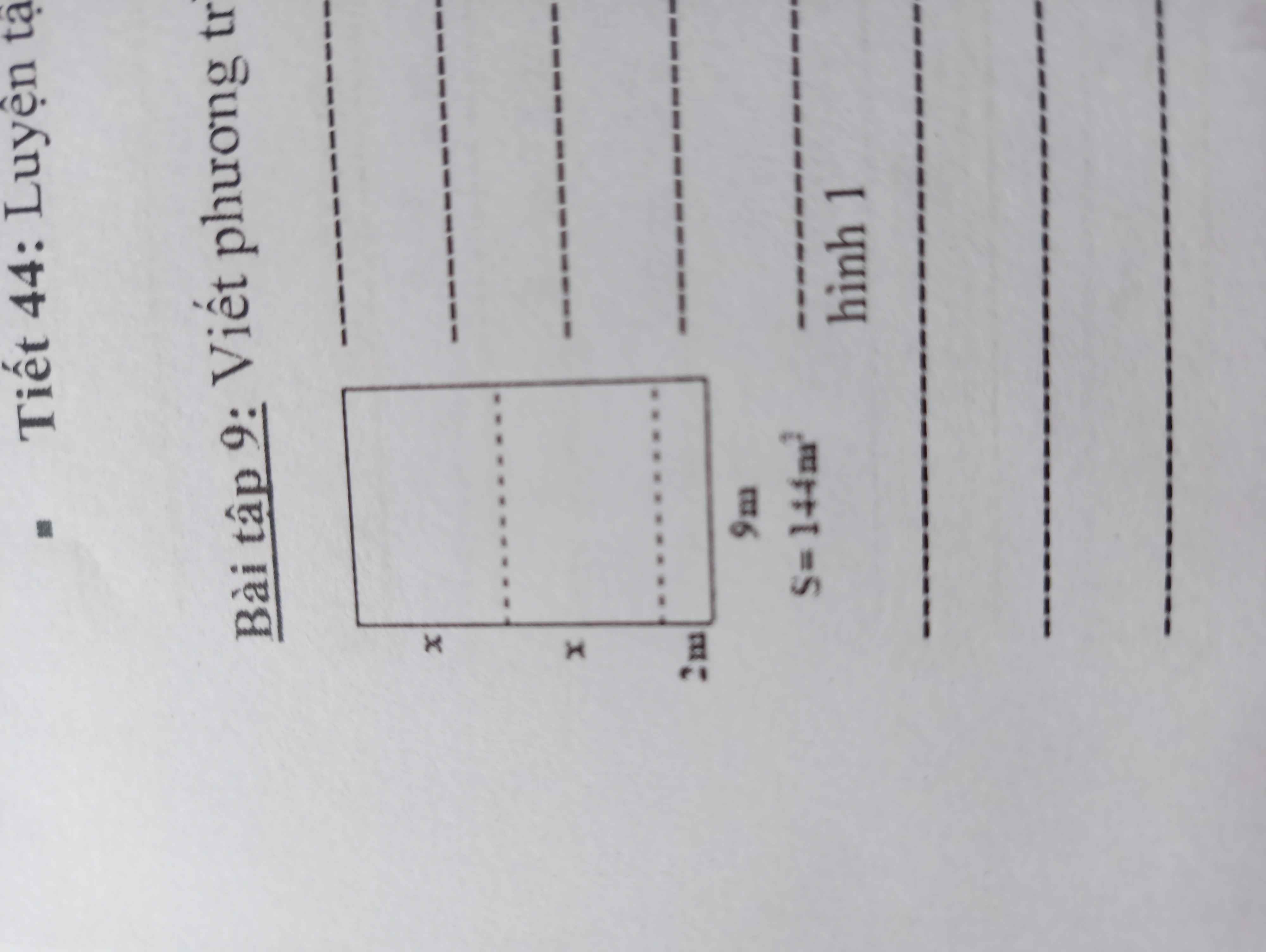
Diện tích hình bên là: \(S=2x.9+2.9=18x+18\)
Ta có: \(S=18x+18=144\Leftrightarrow x=7\left(m\right)\)

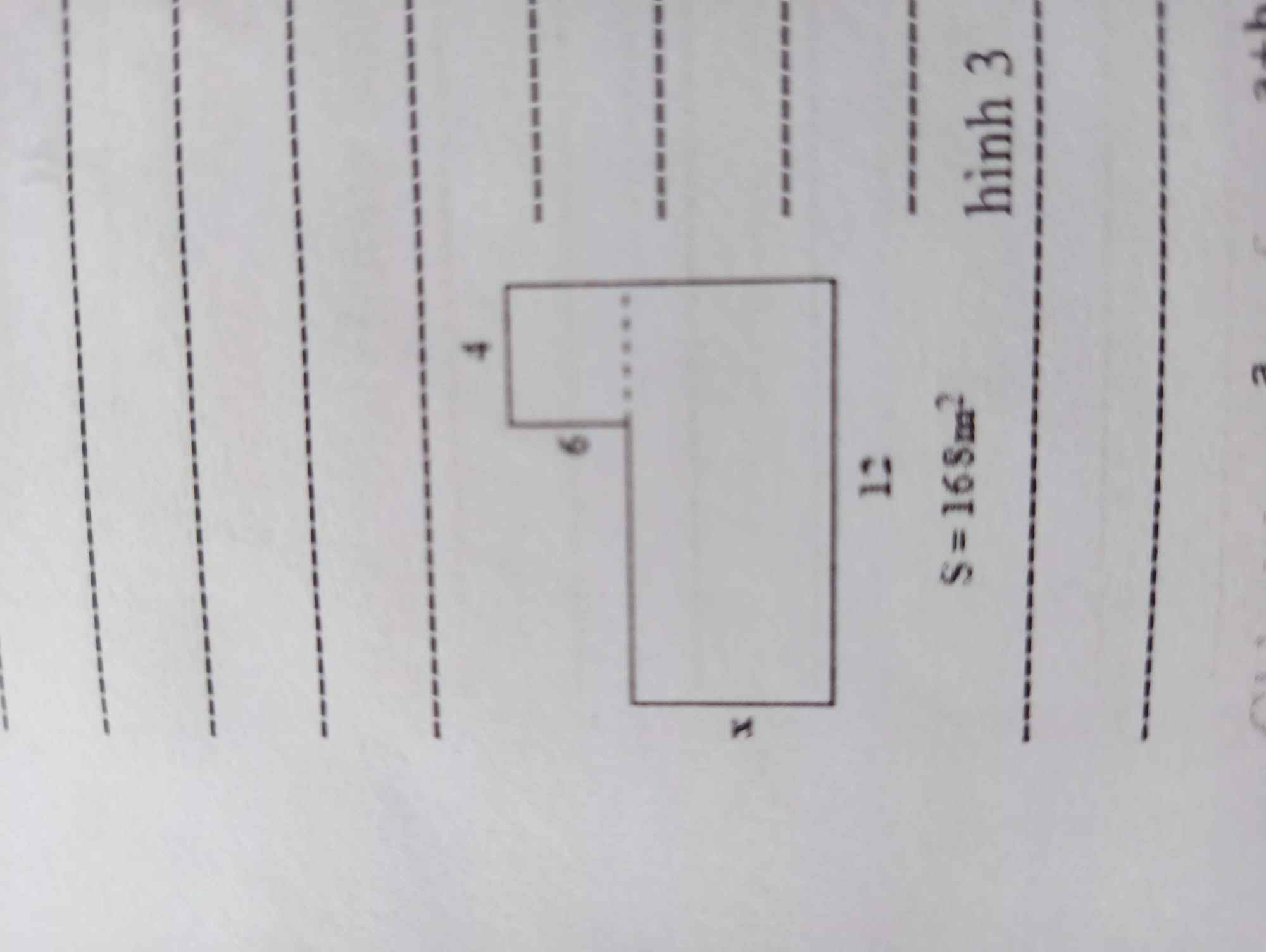
Diện tích hình bên là: \(S=4.6+12.x=24+12x\)
Ta có: \(S=24+12x=168\Leftrightarrow x=12\left(m\right)\)

pt nào v bn
phương trình nào v ạ