Cho hình thang ABCD (AB//CD) gọi I là giao điểm của 2 đường chéo a)CM:IA×ID=IB×IC
b)kẻ IH vuông góc với AB tại I,IK vuông góc với CD tại K.CM IH/IK=AB/CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2022
a, Ta có AB // CD Theo hệ quả Ta lét
\(\dfrac{BI}{ID}=\dfrac{IA}{IC}\Rightarrow BI.IC=IA.ID\)
b, bạn kiểm tra lại đề
22 tháng 2 2022
a. ta có: AB//DC ( gt )
\(\Rightarrow\dfrac{ID}{IB}=\dfrac{IC}{IA}\)
\(\Leftrightarrow ID.IA=IB.IC\)
b,c. ko có điểm O nha pạn ơi
13 tháng 2 2022
a: Xét ΔIAB và ΔICD có
\(\widehat{IAB}=\widehat{ICD}\)
\(\widehat{AIB}=\widehat{CID}\)
Do đó: ΔIAB\(\sim\)ΔICD
Suy ra: IA/IC=IB/ID
hay \(IA\cdot ID=IC\cdot IB\)
b: Điểm O ở đâu vậy bạn?
28 tháng 5 2022
a: Xét ΔIBA và ΔIDC có
\(\widehat{IBA}=\widehat{IDC}\)
\(\widehat{AIB}=\widehat{CID}\)
Do đó: ΔIBA\(\sim\)ΔIDC
b: Ta có: ΔIBA\(\sim\)ΔIDC
nên IB/ID=IA/IC
hay \(IB\cdot IC=IA\cdot ID\)
16 tháng 1 2022
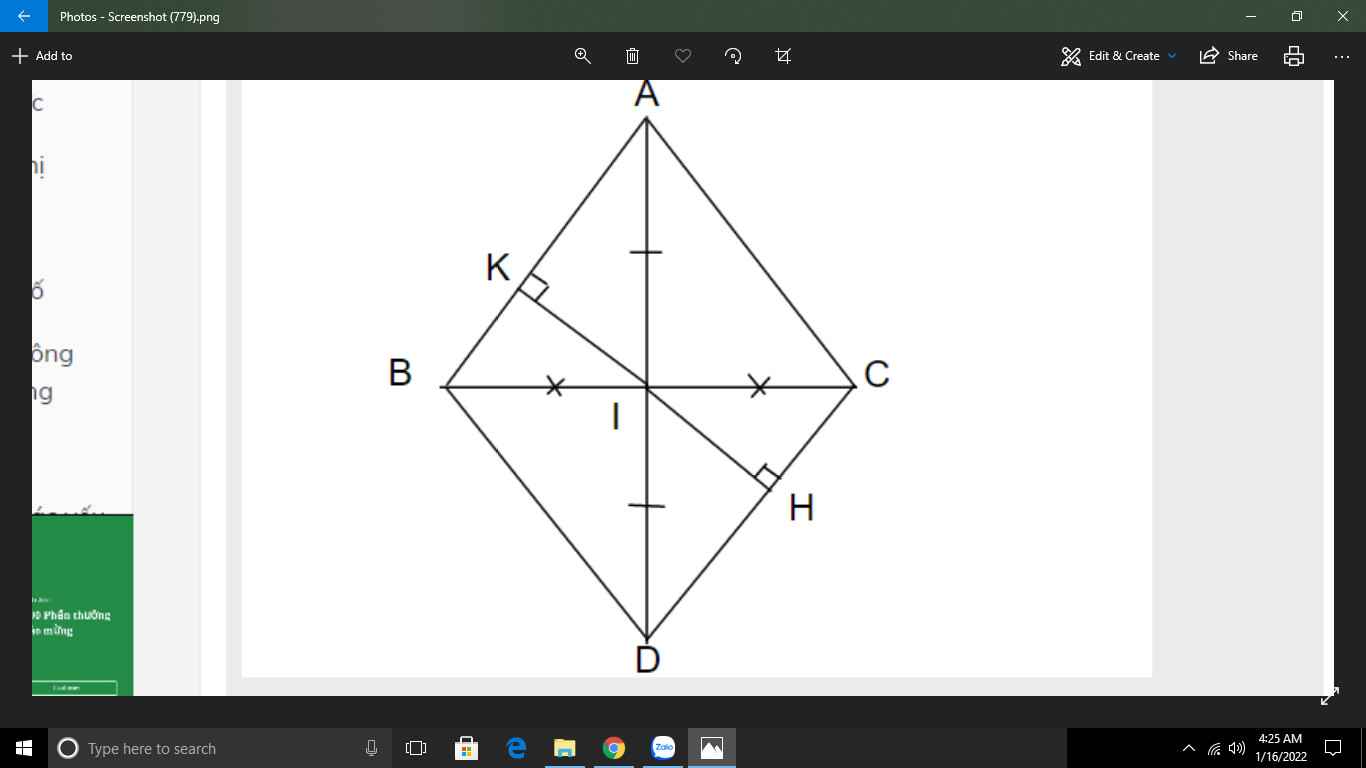
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)
a. ta có: AB//CD ( gt )
Áp dụng hệ quả Ta-lét, ta có:
\(\dfrac{ID}{IB}=\dfrac{IC}{IA}\)
\(\Leftrightarrow IA.ID=IB.IC\)
b. xét tam giác IHA và tam giác IKD có : AH // HD
\(\Rightarrow\dfrac{IH}{IK}=\dfrac{AH}{CK}\) ( ta-lét )
xét tam giác IHB và tam giác IKC có: BH // HC
\(\Rightarrow\dfrac{IH}{IK}=\dfrac{BH}{DK}\) ( ta-lét )
\(\Rightarrow\dfrac{IH}{IK}=\dfrac{AH}{CK}=\dfrac{BH}{DK}\Leftrightarrow\dfrac{IH}{IK}=\dfrac{AH+BH}{CK+DK}\) ( t. chất dãy tỉ số = nhau )
\(\Leftrightarrow\dfrac{IH}{IK}=\dfrac{AB}{CD}\) ( AH+BH = AB; CK + DK = CD )
b, Theo hệ quả Ta lét \(\dfrac{AB}{CD}=\dfrac{AI}{IC}\)(*)
Xét tam giác HIA và tam giác KIC có
^HIA = ^KIC (đối đỉnh)
^IHA = ^IKC = 900
Vậy tam giác HIA ~ tam giác KIC (g.g)
\(\Rightarrow\dfrac{IH}{KI}=\dfrac{AI}{IC}\)(**)
Từ (*) ; (**) suy ra \(\dfrac{IH}{KI}=\dfrac{AB}{CD}\)