làm sao học được lớp học
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-Những việc Q có thể làm: Làm phục vụ ở các quán cơm, làm nhân viên hoặc thực tập sinh của các quán gội đầu, làm móng; làm ở siêu thị, những việc nhẹ nhàng khác,...Làm không quá 8 tiếng 1 ngày, không làm việc nặng. Không làm việc vào ban đêm,...
-Nếu là Q em có thể vừa học vừa làm, chọn một công việc nhẹ nhàng phù hợp với tuổi. Có thể tranh thủi thời gian nghỉ ngơi để học hoặc làm buổi chiều, học vào buổi tối. Chú ý đến sức khoẻ và không làm việc quá sức. Khi kinh tế ổn định trở lại có thể nghỉ làm để chú tâm vào học và ổn định lại sức khoẻ vì vừa học vừa làm dễ gây quá sức dẫn đến uy nhược cơ thể, ảnh hưởng tới dây thần kinh ...
- Theo em Q có thể làm những việc như rửa chén bát, nhân viên siêu thị,... Nhớ là làm vừa khả năng của mình.
- Nếu là Q thì em sẽ tự lập để giúp đỡ cha mẹ. Và không lơ đãng việc học.

Số cách chọn 4 học sinh làm 4 tổ trưởng là: ![]()
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nữ được chọn là ![]()
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nam được chọn là: ![]()
Vậy số cách chọn thỏa yêu cầu bài toán: ![]()
Chọn C.

Gọi số học sinh của ba lớp là \(x;y;z\)
Theo đề bài :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=x+y+z=63\)
Theo dãy tính chất tỉ số bằng nhau ta có :
\(\dfrac{x}{3}+\dfrac{y}{5}+\dfrac{z}{6}=\dfrac{x+y+z}{14}=\dfrac{63}{14}=4,5\)

a:
\(36=2^2\cdot3^2;40=2^3\cdot5\)
=>\(ƯCLN\left(36;40\right)=2^2=4\)
=>\(ƯC\left(36;40\right)=\left\{1;2;4\right\}\)
Nếu muốn chia thành các nhóm sao cho số học sinh nam và nữ trong các nhóm bằng nhau thì số nhóm phải là ước chung của 40 và 36
=>Số nhóm có thể là 1;2;4 nhóm(1)
b: Từ (1) suy ra số nhóm nhiều nhất có thể là 4 nhóm

a) Gọi x là số nhóm học sinh chia được (\(x \in {\mathbb{N}^*}\))
Khi đó x ∈ ƯC(36, 40)
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
=> x ∈ {1; 2; 4}
Vậy có thể chia được thành 1; 2 hoặc 4 nhóm học sinh
b) Số nhóm chia được nhiều nhất là ƯCLN(36, 40) = 4.

20%=1/5
3 học sinh ứng với:1/5-1/8=3/40
số học sinh là:3:3*40=40(HS)
ĐS:40 học sinh

Gọi A là tập hợp mọi cách chọn 4 học sinh trong 12 học sinh
Gọi B là tập hợp cách chọn không thỏa mãn yêu cầu đề bài (tức là chọn đủ học sinh 3 lớp)
Gọi C là tập hợp cách chọn thỏa mãn yêu cầu đề bài
Ta có A = B\(\cup\) C, B \(\cap\) C = \(\varnothing\)
Theo quy tắc cộng ta có
\(\left|A\right|\) = \(\left|B\right|\) + \(\left|C\right|\) \(\Rightarrow\) \(\left|C\right|\) = \(\left|A\right|\) - \(\left|B\right|\) (1)
Dễ thấy \(\left|A\right|\) = \(C_{12}^4\) = 495
Để tính \(\left|B\right|\), ta nhận thấy sẽ chọn một lớp có 2 học sinh, còn 2 lớp còn lại mỗi lớp 1 học sinh. Vì thế theo quy tắc cộng và phép nhân, ta có:
\(\left|B\right|\) = \(C_5^2\)\(C_4^1\)\(C_3^1\) + \(C_5^1\)\(C_4^2\)\(C_3^1\) + \(C_5^1\)\(C_4^1\)\(C_3^2\) = 120 + 90 + 60 = 270
Thay vào (1) ta có \(\left|C\right|\) = 495 - 270 = 225
Vậy có 225 cách chọn.
Số cách chọn 4 học sinh từ 12 học sinh đã cho là : C412=495C124=495
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau :
* Lớp AA có 2 học sinh, các lớp BB, CC mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C25.C14.C13=120C52.C41.C31=120
* Lớp BB có 2 học sinh, các lớp AA, CC mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C15.C24.C13=90C51.C42.C31=90
Lớp CC có 2 học sinh, các lớp AA, BB mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C15.C14.C23=60C51.C41.C32=60
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là :
120+90+60=270120+90+60=270
Vậy số cách chọn phải tìm là : 495−270=225495−270=225 cách.
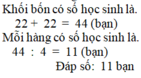
nghe super idol đi