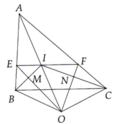
cho tam giác ABC cân tại A có đường phân giác AM.Hai đường cao BE và CF cắt nhau tại H.Chứng minh ba điểm A,H,M thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 6 2023
ΔABC cân tại A
mà AD là trung tuyến
nên AD là đường cao
Xét ΔABC có
AD,BE,CF là các đường cao
BE cắt CF tại H
=>A,H,D thẳng hàng
9 tháng 5 2023
a: Xét ΔDBH vuông tại D và ΔDAC vuông tại D có
góc DBH=góc DAC
=>ΔDBH đồng dạng với ΔDAC
=>DB/DA=DH/DC
=>DB*DC=DA*DH
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
=>ΔAFE đồng dạng với ΔACB
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
7 tháng 1 2022
a/
Ta có
\(\widehat{ABC}=\widehat{ACB}\) (2 góc ở đáy của tg cân ABC) (1)
\(\widehat{ABM}+\widehat{ABC}=\widehat{ACN}+\widehat{ACB}=180^o\)(2)
Từ (1) và (2) \(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\) và \(\Delta ACN\) có
AB=AC (cạnh bên của tg cân ABC)
BM=CN (gt)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
\(\Rightarrow\Delta ABM=\Delta ACN\left(c.g.c\right)\Rightarrow AM=AN\Rightarrow\Delta AMN\)cân tại A
b/
Xét tg vuông BME và tg vuông CNF có
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\Rightarrow\widehat{AMN}=\widehat{ANM}\) (2 góc ở đáy của tg cân AMN)
BM=CN (gt)
\(\Rightarrow\Delta BME=\Delta CNF\) (Hai tg vuông có cạnh huyền và một góc nhọn tương ứng = nhau thì bằng nhau)
c/
Xét tg cân AMN có AM=AN (1)
\(\Delta BME=\Delta CNF\left(cmt\right)\Rightarrow ME=NF\) (2)
Từ (1) và (2) => AM-ME=AN-NF => AE=AF
Xét tg vuông AEO và tg vuông AFO có
AE=AF (cmt)
AO chung
\(\Rightarrow\Delta AEO=\Delta AFO\) (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau thì bằng nhau)
\(\Rightarrow\widehat{OAE}=\widehat{OAF}\) => AO là phân giác của \(\widehat{MAN}\)
d/
Ta có
\(\widehat{HMN}=\widehat{HMA}-\widehat{AMN}=90^o-\widehat{AMN}\)
\(\widehat{HNM}=\widehat{HNA}-\widehat{ANM}=90^o-\widehat{ANM}\)
Mà \(\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{HMN}=\widehat{HNM}\Rightarrow\Delta HMN\) cân tại H
Ta có
\(OE\perp AM;HM\perp AM\)=> OE//HM \(\Rightarrow\widehat{AOE}=\widehat{AHM}\) (góc đồng vị)
Chứng minh tương tự ta cũng có OF//HN \(\Rightarrow\widehat{AOF}=\widehat{AHN}\) (góc đồng vị)
Mà \(\Delta AEO=\Delta AFO\Rightarrow\widehat{AOE}=\widehat{AF}\)
\(\Rightarrow\widehat{AHM}=\widehat{AHN}\)=> HO là phân giác của \(\widehat{MHN}\)
Xét tg cân HMN có
HO là phân giác của \(\widehat{MHN}\)=> HO là đường trung trực của tg HMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(HO\perp MN\) tại trung điểm của MN
Xét tg cân AMN có
AO là đường phân giác của \(\widehat{MAN}\) (cmt) => AO là đường trung trực của tg AMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(AO\perp MN\) tại trung điểm của MN
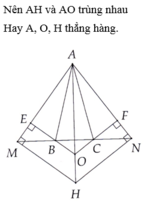
=> AO trung HO (Từ 1 điểm trên đường thẳng chỉ duy nhất dựng được 1 đường thẳng vuông góc với đường thẳng đã cho)
=> A; O; H thẳng hàng
ΔABC cân tại A
mà AD là phân giác
nên AD là đường cao
Xét ΔABC có
AD,BE,CF là các đường cao
BE cắt CF tại H
=>A,H,D thẳng hàng