Giải các phương trình bằng cách sử dụng các hằng đẳng thức.
Giúp với ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(8x^3+12x^2+6x+1=\left(2x+1\right)^3\)
\(=\left(2\cdot24.5+1\right)^3=50^3=125000\)

Do \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall x\) nên BPT tương đương:
\(-3\left(x^2+x+1\right)\le x^2-3x-1\le3\left(x^2+x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-1\ge-3x^2-3x-3\\x^2-3x-1\le3x^2+3x+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x^2\ge-2\left(luôn-đúng\right)\\2x^2+6x+4\ge0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ge-1\\x\le-2\end{matrix}\right.\)

c) \(\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
c) \(\left(x^2+3^2\right)^2=x^4+18x+81\)
c) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
c) \(\left(3x-y^2\right)^2=9x^2-6xy^2+y^4\)
c) \(\left(x+2y^2\right)^2=x^2+4xy^2+4y^4\)
c) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
c) \(\left(2x+3y^2\right)^2=4x^2+12xy^2+9y^4\)
c) \(\left(4x-2y^2\right)^2=16x^2-16xy^2+4y^4\)
c) \(\left(4x^2-2y\right)^2=16x^4-16x^2y+4y^2\)
c) \(\left(\dfrac{1}{x}-5\right)\left(\dfrac{1}{x}+5\right)=\dfrac{1}{x^2}-25\)
c) \(\left(x-\dfrac{3}{2}\right)\left(x+\dfrac{3}{2}\right)=x^2-\dfrac{9}{4}\)
c) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
c) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
c) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)=\dfrac{y^2}{9}-\dfrac{x^2}{4}\)
c) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=4x^2-\dfrac{4}{9}\)
c) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\dfrac{9}{25}-4x^2\)
c) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{4}+\dfrac{1}{2}x\right)=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
c) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)

( a + b )3 - ( a3 + b3 )
= a3 + 3a2b + 3ab2 + b3 - a3 - b3
= 3a2b - 3ab2
= 3ab ( a + b )

Bài 5:
1) \(\left(5+7\right)\left(7-5\right)=7^2-5^2\)
2) \(\left(x+y\right)\left(y-x\right)=y^2-x^2\)
3) \(\left(x-y\right)\left(-x-y\right)=-\left(x+y\right)\left(x-y\right)=-\left(x^2-y^2\right)=y^2-x^2\)
6) \(\left(2+3x^2\right)\left(3x^2-2\right)=9x^4-4\)
7) \(\left(\dfrac{1}{2}+x\right)\left(-x+\dfrac{1}{2}\right)=\left(\dfrac{1}{2}+x\right)\left(\dfrac{1}{2}-x\right)=\dfrac{1}{4}-x^2\)
8) \(\left(4m-5n\right)\left(5n+4m\right)=\left(4m-5n\right)\left(4m+5n\right)=16m^2-25n^2\)
9) \(\left(7a+1\right)\left(1-7a\right)=\left(1+7a\right)\left(1-7a\right)=1-49a^2\)
10) \(\left(1+9\right)\left(1-9\right)=1-9^2\)

(x - 2)2 = 7/2 ⇔ x - 2 = ±√(7/2) ⇔ x = 2 ± √(7/2)
Vậy phương trình có hai nghiệm
x1 = 2 + √(7/2); x2 = 2 - √(7/2)

( x - 2 ) 2 = 7 / 2
⇔ x - 2 = ±√(7/2)
⇔ x = 2 ± √(7/2)
Vậy phương trình có hai nghiệm
x 1 = 2 + √ ( 7 / 2 ) ; x 2 = 2 - √ ( 7 / 2 )

\(\left(a^2-1\right)\left(a^2-a+1\right)\left(a^2+a+1\right)=\left(a-1\right)\left(a^2+a+1\right)\left(a+1\right)\left(a^2-a+1\right)\)
\(=\left(a^3-1\right)\left(a^3+1\right)=a^6-1\)

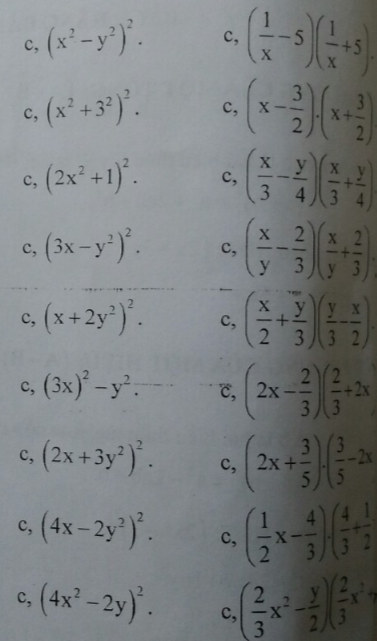 viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp 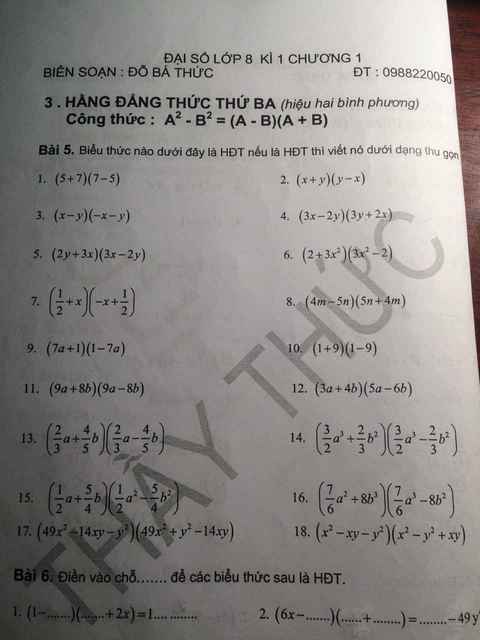
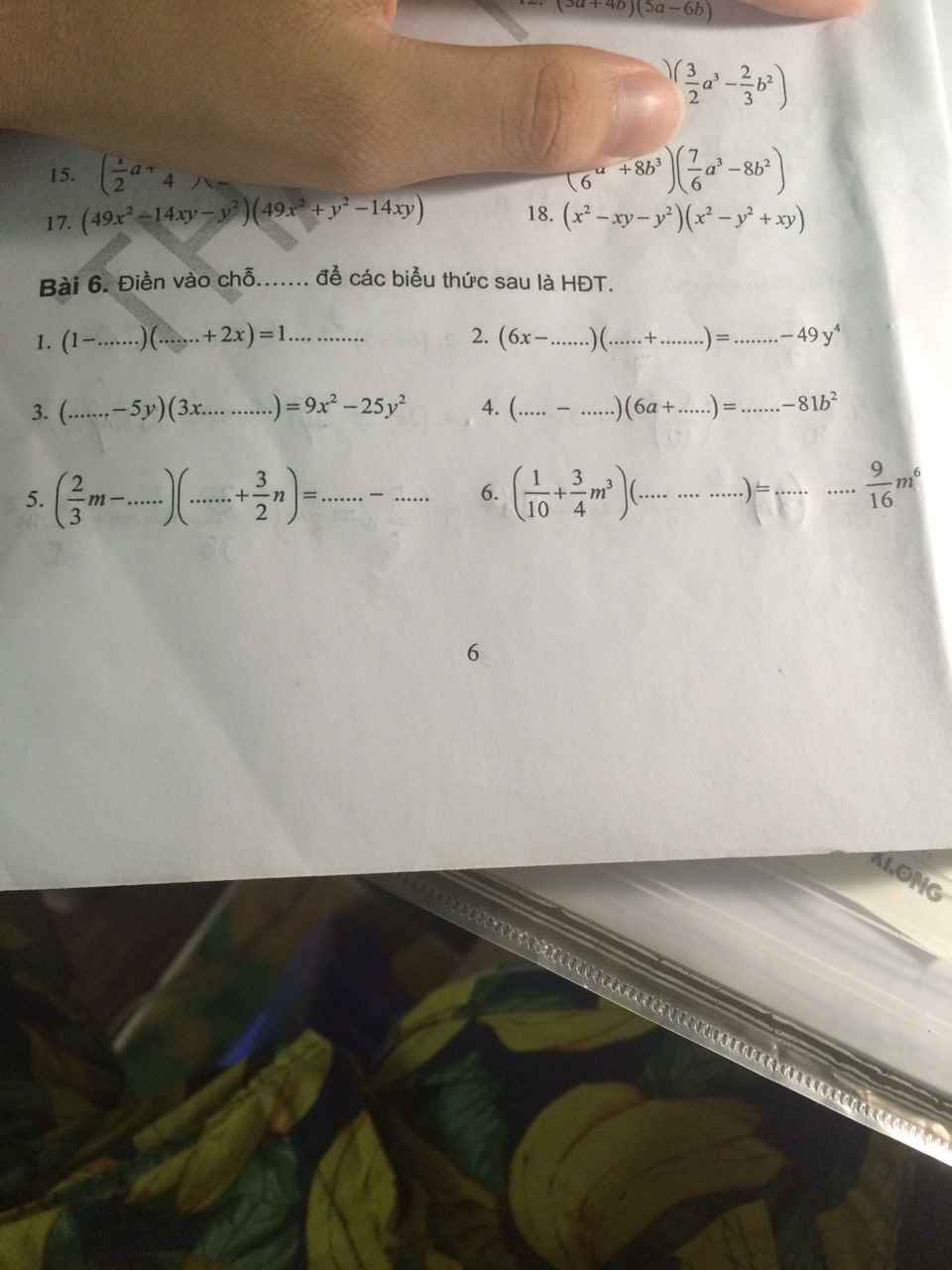
\(\left(4A\right)\\ a,\\ \Leftrightarrow\left[\left(x-2\right)\left(2x+3\right)\right]\left[\left(x-2\right)\left(2x+3\right)\right]=0\\ \Leftrightarrow\left(-x-5\right)\left(3x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-x-5=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{-1}{3}\end{matrix}\right.\\ b,\\ \Leftrightarrow\left[3\left(2x+1\right)\right]^2-\left[2\left(x+1\right)\right]^2=0\\ \Leftrightarrow\left[3\left(2x+1\right)-2\left(x+1\right)\right]\left[3\left(2x+1\right)+2\left(x+1\right)\right]=0\\ \Leftrightarrow\left(4x+1\right)\left(8x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+1=0\\8x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{4}\\x=\dfrac{-5}{8}\end{matrix}\right.\\ c,\\ \Leftrightarrow\left[\left(x+1\right)+1\right]^2=0\\ \Leftrightarrow\left(x+1\right)+1=0\\ \Leftrightarrow x+2=0\Rightarrow x=-2\\ d,\\ \Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x+3\right)+\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left[\left(x-1\right)\left(x+3\right)+1\right]=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\\left(x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
\(\left(4B\right)\\ a,\\ \Leftrightarrow49-14x+x^2-4\left(x+25\right)^2=0\\ \Leftrightarrow49-14x+x^2-4x^2-40x-100=0\\ \Leftrightarrow3x^2-54x-51=0\\ \Leftrightarrow-3\left(x^2+18x+17\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+17\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+17=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-17\end{matrix}\right.\\ b,\\ \Leftrightarrow4x^2\left(x^2-2x+1\right)-\left(4x^2+4x+1\right)=0\\ \Leftrightarrow x^2-6x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
\(c,\\ \Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(2-x\right)=0\\ \Leftrightarrow\left(x+1\right)\left[\left(x^2-x+1\right)-\left(2-x\right)\right]=0\\ \Leftrightarrow\left(x+1\right)\left(x^1-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=-1\end{matrix}\right.\\ d,\\ \Leftrightarrow\left(x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
hum được học on mà lắm bài nên ít tg làm