giúp minh với cần lắm r ạ:((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
MA
1
9 tháng 12 2021
\(P=\dfrac{x^3+8y^3}{4^3+4^3}=\dfrac{\left(x+2y\right)^3-3\cdot x\cdot2y\cdot\left(x+2y\right)}{128}\)
\(=\dfrac{\left(-8\right)^3-6\cdot\left(-6\right)\cdot\left(-8\right)}{128}=\dfrac{128-6\cdot48}{128}=-\dfrac{5}{4}\)
12 tháng 11 2021
1. What's your address?
2. ......better than coffee
3......... most important in life
4........thirty- minute break.
8 tháng 5 2021
ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}
KH
8 tháng 5 2021
Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
TM
8 tháng 5 2021
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....
2 tháng 12 2021
\(B=1+4+4^2+...+4^{11}\)
\(\Rightarrow B=\left(1+4\right)+\left(4^2+4^3\right)+...+\left(4^{10}+4^{11}\right)\)
\(\Rightarrow B=\left(1+4\right)+4^2\left(1+4\right)+...+4^{10}\left(1+4\right)\)
\(\Rightarrow B=\left(1+4\right)\left(4^2+...+4^{10}\right)\)
\(\Rightarrow B=5\left(4^2+...+4^{10}\right)⋮5\)
\(B=1+4+4^2+...+4^{11}\)
\(\Rightarrow B=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)...+\left(4^9+4^{10}+4^{11}\right)\)
\(\Rightarrow B=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)...+4^9\left(1+4+4^2\right)\)
\(\Rightarrow B=\left(1+4+4^2\right)\left(4^3+...+4^9\right)\)
\(\Rightarrow B=21\left(4^3+...+4^9\right)⋮21\)
bạn vẽ nốt hình đi để mình giúp nhé
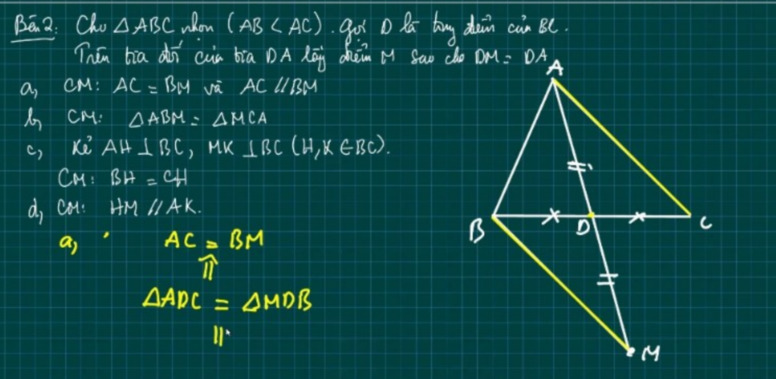
a: Xét tứ giác ABMC có
D là trung điểm của AM
D là trung điểm của BC
Do đó: ABMC là hình bình hành
Suy ra: AC//BM và AC=BM
b: Xét ΔABM và ΔMCA có
AB=MC
BM=CA
AM chung
Do đó: ΔABM=ΔMCA
c: Xét ΔBHA vuông tại H và ΔCKM vuông tại K có
BA=CM
\(\widehat{ABH}=\widehat{MCK}\)
Do đó: ΔBHA=ΔCKM
Suy ra: BH=CK