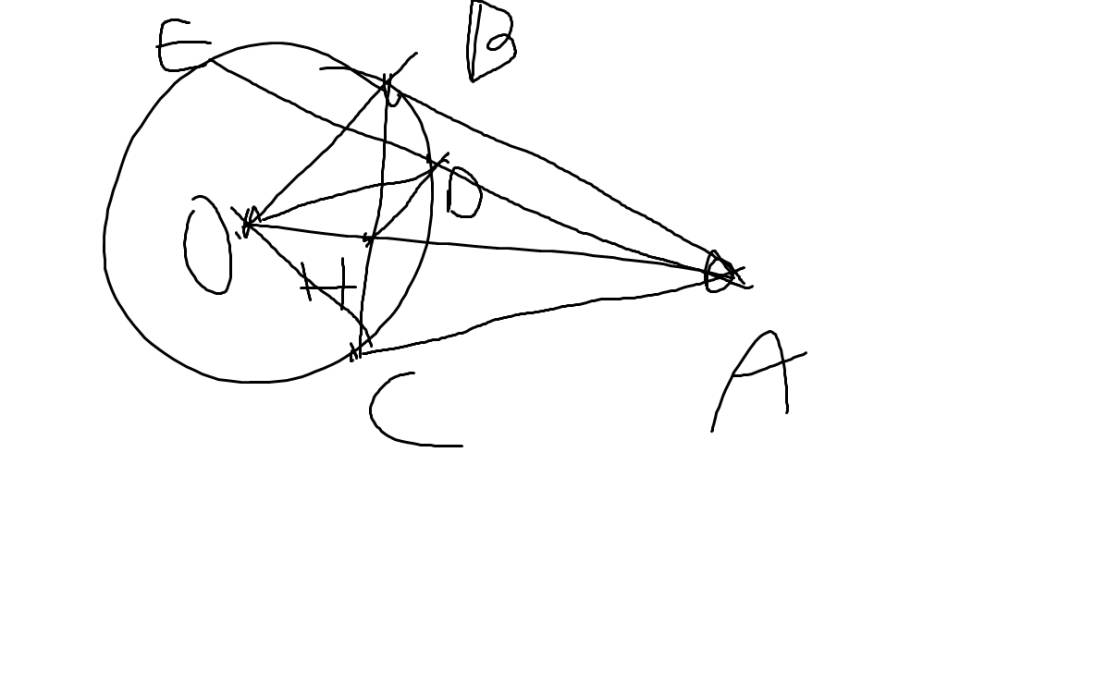
Từ một điểm 4 nằm ngoài đường tròn ( O ; R ) với O4 < 2R . Vẽ hai tiếp tuyến AD , AE với ( O ) ( D , E là các tiếp điểm ) . Gọi H là giao điểm của DE và AO . Lấy điểm M thuộc cung nhỏ DE ( M khác D khác E , MD < ME ) . Tia M cắt đường tròn ( O , R ) tại V. Đoạn tháng 40 cắt cung nhỏ DE tại K. a ) Chứng minh AOLDE và AD = AMAN b ) Chứng minh NK là tia phân giác của góc . DVE và tứ giác NHON nổi tiếp . c ) Kẻ đường kính KQ của đường tròn ( O , R ) . Tia QN cắt tia ED tại C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O
Mà \(OH\perp BE\) (giả thiết) \(\Rightarrow OH\) là đường cao đồng thời là trung trực của BE
Hay OA là trung trực của BE
\(\Rightarrow AB=AE\)
Xét hai tam giác OAB và OAE có: \(\left\{{}\begin{matrix}OB=OE=R\\AB=AE\left(cmt\right)\\OA\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAB=\Delta OAE\left(c.c.c\right)\)
\(\Rightarrow\widehat{AEO}=\widehat{ABO}=90^0\Rightarrow AE\) là tiếp tuyến của (O)

a: Xét tứ giác OMAN có
\(\widehat{OMA}+\widehat{ONA}=180^0\)
Do đó: OMAN là tứ giác nội tiếp

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
c: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{HAE}\) chung
Do đó: ΔAEH\(\sim\)ΔAOD
Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)

Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,C,O cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD